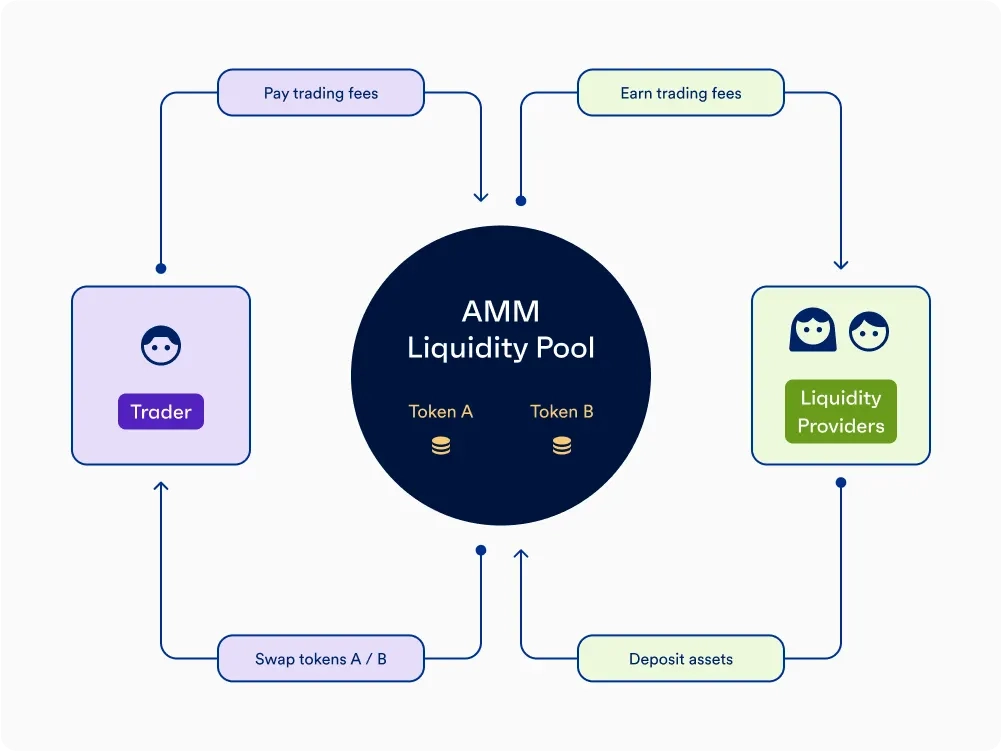
【AMM量化深潜01】理解 AMM 的经济学本质：从无常损失 (IL) 到再平衡损失 (LVR)

许多人将链上交易所（DEX）如Uniswap 的流动性提供（LP）视为一种被动的“理财”或“挖矿”行为，但这是一种极其危险的误解。从市场微观结构来看，AMM 本质上是一个 由算法定义的逆向选择（Adverse Selection）博弈场。

本文是【AMM 量化深潜】系列的第一篇。我们将摒弃传统的散户视角，从宏观市场均衡出发，通过严谨的数学推导剥离“无常损失（IL）”的伪装，引出专业视角下真正的 AMM 做市核心风险度量——再平衡损失（Loss-Versus-Rebalancing, LVR）。

引言

随着 DeFi 的繁荣与链上自动做市商（AMM, Automated Market Maker）机制的兴起，我们正处于一场金融基础设施的范式转移之中。这不仅是技术的迭代，更是一股不可逆转的历史潮流。

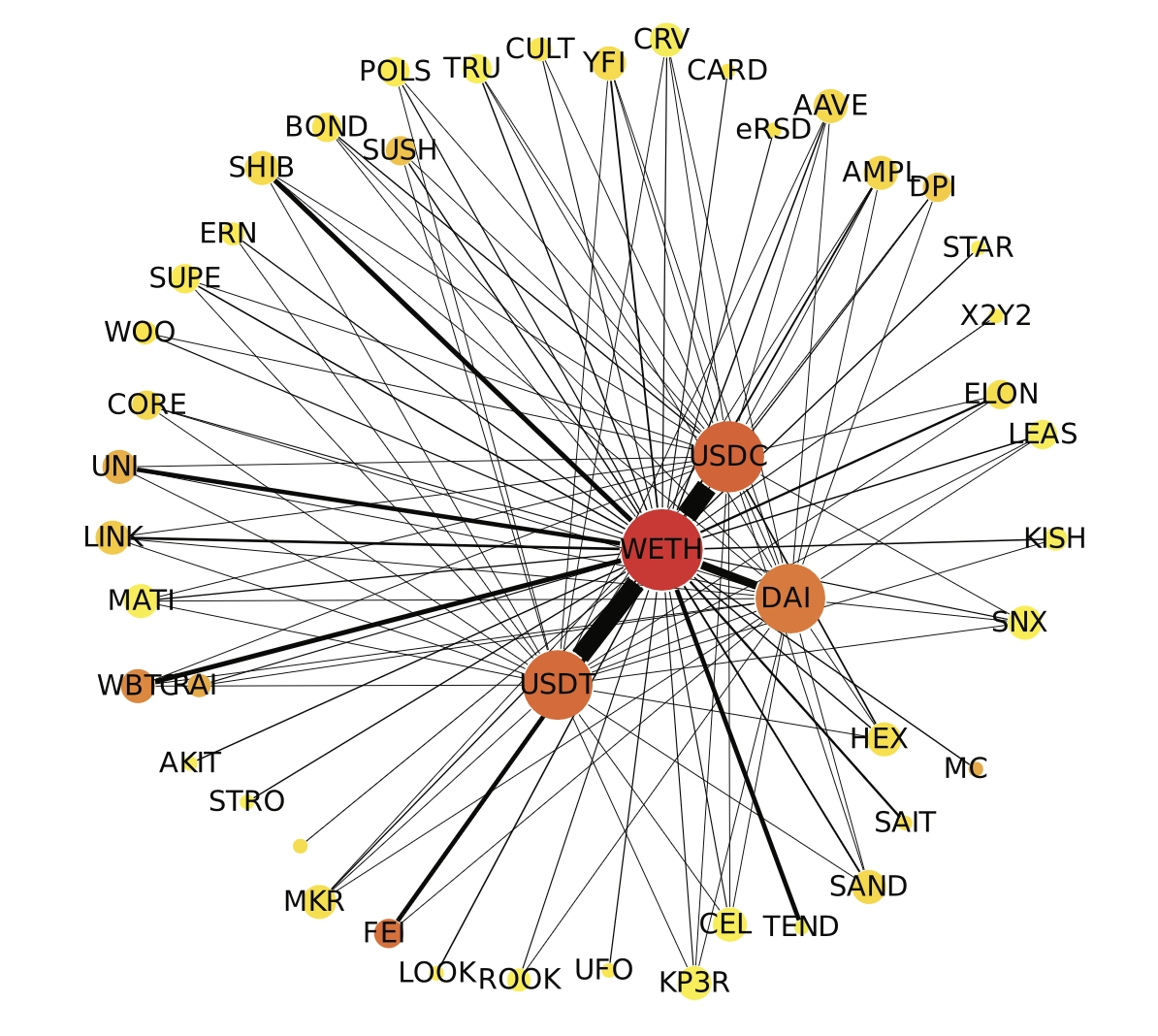
然而，在这场浪潮中，即使是许多专业的量化从业者，在审视 Uniswap 等协议时，往往也容易陷入中心化交易所的思维定势。

如果我们仅仅停留在“存币生息”的收益率表象，或者还在使用“无常损失（Impermanent Loss, IL）”这种路径无关的指标来衡量风险，那么我们不仅严重低估了尾部风险，更错失了对这一新兴市场微观结构的本质认知。

宏观视角：AMM 的经济学原理

直观理解

从更熟悉的传统金融的限价订单薄（Limit Order Book, LOB）理解 AMM 会更加容易。在传统的限价订单簿（LOB）市场中，做市商（Market Maker）通过在当前价格的上方挂卖单（Ask），在下方挂买单（Bid）来提供流动性。这一报价是由做市商实时动态调整的。

AMM（自动做市商）本质上是一个通过算法自动维护的订单薄。在 AMM（特别是恒定乘积做市商）中，流动性提供者（LP）是被动的。如 Uniswap V2 的经典模型 \(x \cdot y = k\) 中，流动性均匀分布在 \((0, \infty)\) 的价格区间上。这意味着，无论价格涨到 ¥1000 还是跌到 ¥0.01，池子里永远有资产可供交易。这在数学上等价于你在订单薄上的每一个价位都挂了无限小的买单和卖单。此时，价格的发现完全依赖于外部套利者。

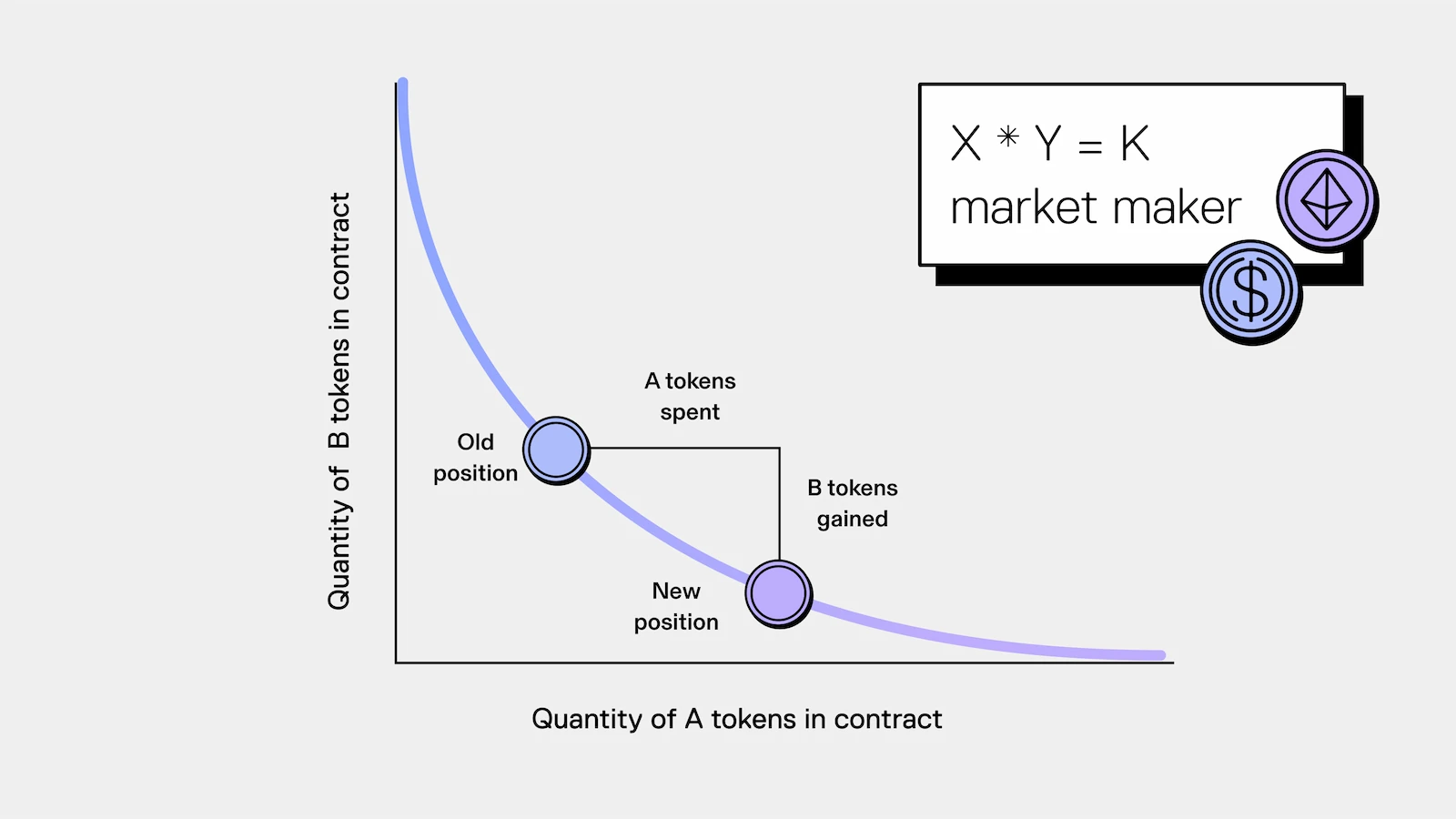
内生均衡

Lehar & Parlour 的核心贡献在于将 AMM 的流动性供给看作一个内生变量。池子的大小不是随机的，而是 LP 和套利者之间博弈的纳什均衡。

设定场景

当外部市场价格发生跳变（Innovation）时，AMM 的报价是滞后的。套利者会通过一笔交易将 AMM 的价格推至与外部市场一致。

• LP 的收益 (\(\Pi_{LP}\))：来源于交易产生的交易费。
• LP 的成本 (\(L_{arb}\))：来源于当外部价格发生跳变（Innovation）时，套利者（Arbitrageur）进场搬砖造成的损失（即逆向选择成本）。

自由进出条件：只要预期收益 \(\Pi_{LP} > 0\)，就会有新的资金进入池子；反之则退出。因此，均衡状态下 \(\Pi_{LP} = 0\)（考虑机会成本后）。

关键机制：价格冲击 (Price Impact) 是调节阀

在 AMM 中，价格冲击是确定性的，由池子深度（\(T_0\)）决定。

• 池子越大 (\(T_0 \uparrow\)) \(\rightarrow\) 价格冲击越小。
• 池子越小 (\(T_0 \downarrow\)) \(\rightarrow\) 价格冲击越大。

套利者的利润最大化问题

假设外部价格发生了一个跳变 \(\sigma\)。套利者需要决定交易多少量 (\(t_{arb}\)) 来最大化自己的利润。
套利者的利润函数 \(\pi_{arb}\) 是：

$$ \pi_{arb} = \underbrace{(\text{新价格} - \text{成交均价})}_{\text{价差收益}} \times t_{arb} $$

由于成交均价取决于交易量 \(t_{arb}\) 和池子深度 \(T_0\)，池子越大，成交均价越接近旧价格，套利者的利润空间就越大。

结论 A： 池子深度 \(T_0\) 越大，套利者为了消除价差，最优交易量 \(t_{arb}^*\) 就会越大。

$$ \frac{\partial t_{arb}^*}{\partial T_0} > 0 $$

LP 的损失函数

LP 的损失直接等于套利者的利润（在零和博弈假设下）。

$$ L_{arb} \propto t_{arb}^* \times \sigma $$

结合结论 A，我们得到一个反直觉但至关重要的推论：池子越深，LP 在单次价格跳变中遭受的损失总额越大。（因为套利者能以更有利的价格吃掉更多的单）。

均衡推导

LP 的净收益函数：

$$\text{Net Profit} = \text{Fees}(T_0) - \underbrace{\text{Loss}(T_0, \sigma)}_{L_{arb} \propto t_{arb}^* \times \sigma}$$

• 波动率 \(\sigma\) 的影响：当波动率 \(\sigma\) 上升，Loss 项急剧增加。为了维持 Net Profit = 0，必须通过减小 \(T_0\) 来增加价格冲击，从而迫使套利者减少交易量 \(t_{arb}^*\)，进而降低 Loss。

  $$ \sigma \uparrow \Rightarrow \text{Equilibrium } T_0 \downarrow $$

• 噪音交易的影响：当噪音交易量增加，Fees 项增加。LP 有利可图，资金涌入，导致 \(T_0\) 增加，直到边际收益再次为零。

  $$ \text{Noise} \uparrow \Rightarrow \text{Equilibrium } T_0 \uparrow $$

小结： 均衡池规模是 LP 为了“防御”套利者而自发形成的一种阻力机制。高波动率下池子变浅，本质上是 LP 在通过提高滑点（价格冲击）来逼退套利者。这解释了为什么在高波动性资产中，Uniswap 的滑点往往较大（池子浅），而在稳定币对中滑点极小。LP 实际上是在用噪音交易的费用补贴套利者的利润。

Lehar & Parlour 在其论文中给出了均衡状态下代币供应量 \(T_0\) 的闭式解，它量化了“收益”与“攻击成本”的精确平衡：

$$ T_{0} = q \cdot \left[ \sqrt{1 + \frac{(1-\alpha)^{2} \tau^{2} p_{0}^{2}}{\alpha^{2} \omega^{2}}} - \frac{(1-\alpha) \tau p_{0}}{\alpha \omega} \right] $$

（其中 \(q\) 为噪音交易量，\(\alpha\) 为跳价概率，\(\omega\) 包含了波动率 \(\sigma\)）

即使不深究每个参数，我们也能从结构中一眼看出：池子规模 \(T_0\) 与噪音交易量 \(q\) 成正比（分子），且受到波动率 \(\sigma\) 的强烈抑制（分母中的 \(\omega\) 含 \(\sigma\)）。 这就是量化视角的“市场微观结构”。

传统度量的缺陷：无常损失 (IL) 的数学本质

再深入了解一些，一定会了解到DEX做市的风险：无常损失（Impermanent Loss, IL）。为什么叫这个名字呢？他们会告诉你：“只要价格回去，就没损失。” 但这一描述实在很没意义——只要手里有头寸，只要市场在运行，有什么损失不是无常的呢？它假设价格最终会回归起点，且忽略了价格路径中的波动成本。

IL 的严格定义

考虑一个恒定乘积 \(xy=L^2\) 的池子，其中 \(L\) 为流动性，\(P = y/x\) 为价格。
LP 持仓价值 \(V_{pool}\) 与价格 \(P\) 的关系为：

$$ V_{pool}(P) = y + xP = L\sqrt{P} + \frac{L}{\sqrt{P}} \cdot P = 2L\sqrt{P} $$

对比“持有不动（HODL）”策略的价值 \(V_{hold}\)（假设初始价格为 \(P_0\)）：

$$ V_{hold}(P) = y_0 + x_0 P = L\sqrt{P_0} + \frac{L}{\sqrt{P_0}} P = L\sqrt{P_0} (1 + \frac{P}{P_0}) $$

无常损失 \(IL(P)\) 定义为两者之差：

$$ IL(P) = \frac{V_{pool}(P) - V_{hold}(P)}{V_{hold}(P)} = \frac{2\sqrt{\rho}}{1+\rho} - 1 $$

其中 \(\rho = P/P_0\) 是价格比率。

对于无常损失 \(IL(P)\)，其公式只依赖于当前价格 \(P_t\) 和初始价格 \(P_0\)，这意味着无论中间价格经历了多么剧烈的波动（例如 \(100 \to 50 \to 200 \to 100\)），只要终点 \(P_T = P_0\)，计算出的 \(IL(P_T)\) 恒等于 0。Alexander & Fritz 指出，IL 的最大问题在于它是 路径无关（Path Independent） 的。在这个过程中，LP 实际上已经被套利者来回“收割”了两次。IL 掩盖了这种持续的出血。

IL 的泰勒展开

当价格变化很小（\(P \approx P_0\)）时，我们可以对 IL 进行泰勒展开。令 \(P = P_0(1+r)\)，其中 \(r\) 为收益率。

$$ V_{pool} \approx 2L\sqrt{P_0}(1 + \frac{r}{2} - \frac{r^2}{8}) $$

$$ V_{hold} = 2L\sqrt{P_0}(1 + \frac{r}{2}) $$

两者相减，二阶项即为 IL 的近似值：

$$ IL \approx -\frac{1}{8} r^2 \cdot V_{0} $$

这个式子揭示了 LP 头寸的局部几何性质：它具有负凸性（Negative Convexity / Short Gamma）。这意味着：只要价格发生微小变动 \(\Delta P\)，LP 必定遭受损失，且损失与变动幅度的平方成正比。

矛盾

既然每一刻都在亏，为什么 IL 可能是 0？这就是本文的核心逻辑转折点。

• 微观上（泰勒展开）： 每一笔导致价格变化的交易，LP 都在亏损（卖飞买套）。
• 宏观上（IL 公式）： 如果价格回到原点，LP 似乎没亏。

当价格从 \(P_0\) 涨到 \(P_1\) 时，LP 被迫以低于市价卖出资产，遭受了逆向选择损失；当价格从 \(P_1\) 跌回 \(P_0\) 时，LP 又被迫以高于市价买回资产，再次遭受了损失。

所谓的“无常损失为 0”，仅仅是指LP的账面价值相对于“持有不动”策略持平。但实际上，LP 在 \(P_0 \to P_1\) 被套利者收割了一次，在 \(P_1 \to P_0\) 又被套利者收割了一次。这种持续的被收割才是 LP 真正的经营成本，不能因为账面价值回归就忽略它。

结论： 泰勒展开证明了 LP 在每一瞬间都面临 Gamma 风险（\(-\frac{1}{8}\sigma^2\)），而“路径无关”的 IL 掩盖了这些瞬时风险在时间轴上的累积。

核心变革：再平衡损失 (LVR) 的推导

为了捕捉路径依赖的风险，我们需要引入新的风险度量：LVR (Loss-Versus-Rebalancing)

LVR 的核心思想是：如果我们想要通过动态对冲来完全消除价格风险（Delta Neutral），我们需要构建一个对冲组合。LP 头寸价值与该对冲组合价值之间的差额，就是 LVR。

LVR 数学推导

为了量化 LP 相对于“主动再平衡策略”的损失，我们需要在一个连续时间的框架下，利用随机微积分来拆解 LP 头寸的价值变化。

设定价格过程与随机环境

假设风险资产的价格 \(P_t\) 服从几何布朗运动 (Geometric Brownian Motion, GBM)。为了聚焦于波动率带来的损耗，我们假设无风险利率为 0。价格的随机微分方程（SDE）为：

$$ \frac{dP_t}{P_t} = \sigma dW_t \quad \Rightarrow \quad dP_t = \sigma P_t dW_t $$

其中 \(\sigma\) 为常数波动率，\(W_t\) 为标准布朗运动。
根据伊藤规则 (Itô’s rule)，二阶变分项为：

$$ (dP_t)^2 = \sigma^2 P_t^2 dt $$

(注：这是后续计算 Gamma 损耗项的关键基础)

LP 头寸的价值函数与 Greeks

在恒定乘积做市商 (CPMM, \(x \cdot y = L^2\)) 中，LP 的头寸价值 \(V(P_t)\) 以计价货币（Numéraire, 通常是稳定币）表示为：

$$ V(P_t) = y_t + x_t P_t = L\sqrt{P_t} + \frac{L}{\sqrt{P_t}} \cdot P_t = 2L\sqrt{P_t} $$

我们需要计算该价值函数对价格的一阶导数（Delta）和二阶导数（Gamma）：

• Delta (\(\Delta_t\)): 衡量头寸价值对价格的敏感度。

$$ \Delta_t = \frac{\partial V}{\partial P} = \frac{d}{dP}(2L P^{1/2}) = L P^{-1/2} = \frac{L}{\sqrt{P}} = x_t $$

(注：这里清晰地表明，LP 的 Delta 正好等于其当前持有的风险资产数量 \(x_t\))

• Gamma (\(\Gamma_t\)): 衡量 Delta 对价格的敏感度（即凸性）。

$$ \Gamma_t = \frac{\partial^2 V}{\partial P^2} = \frac{d}{dP}(L P^{-1/2}) = -\frac{1}{2} L P^{-3/2} $$

(注：二阶导数为负，证明 LP 本质上是在做空 Gamma。当价格波动时，LP 总是“高买低卖”——价格上涨时 Delta 减小（卖出），价格下跌时 Delta 增加（买入），这是亏损的根源)

LP 价值变化的伊藤展开 (Itô Expansion)

根据伊藤引理 (Itô’s Lemma)，函数 \(V(P_t)\) 的微分 \(dV_t\) 展开为：

$$ dV_t = \frac{\partial V}{\partial P} dP_t + \frac{1}{2} \frac{\partial^2 V}{\partial P^2} (dP_t)^2 $$

将上述计算得到的 Delta、Gamma 以及 \((dP_t)^2 = \sigma^2 P_t^2 dt\) 代入公式：

$$ dV_t = \underbrace{x_t dP_t}_{\text{Delta Term}} + \underbrace{\frac{1}{2} \left( -\frac{1}{2} L P_t^{-3/2} \right) (\sigma^2 P_t^2 dt)}_{\text{Gamma Term}} $$

关键步骤：Gamma 项的化简与重构
为了看清损耗的本质，我们需要对第二项（Gamma 项）进行代数变形：

1. 合并指数项：\(P_t^{-3/2} \cdot P_t^2 = P_t^{1/2} = \sqrt{P_t}\)
2. 整理系数：\(\frac{1}{2} \cdot (-\frac{1}{2}) \cdot \sigma^2 = -\frac{\sigma^2}{4}\)
3. 代入原式：\(\text{Gamma Term} = -\frac{\sigma^2}{4} L \sqrt{P_t} dt\)
4. 利用价值公式代换：由于 \(V_t = 2L\sqrt{P_t}\)，可得 \(L\sqrt{P_t} = \frac{1}{2} V_t\)。将其代入上式：

   $$ -\frac{\sigma^2}{4} \left( \frac{1}{2} V_t \right) dt = -\frac{\sigma^2}{8} V_t dt $$

最终，我们得到了 LP 头寸价值动态的精简表达式：

$$ \boxed{dV_t = x_t dP_t - \frac{\sigma^2}{8} V_t dt} $$

这个公式揭示了 LP 价值变化的两个独立来源：

1. 市场风险 (\(x_t dP_t\))：这部分包含 \(dW_t\) 随机项，随价格波动，期望为 0。
2. 确定性漂移 (\(-\frac{\sigma^2}{8} V_t dt\))：这是一个恒为负的时间项。只要波动率 \(\sigma > 0\)，这部分价值就会随着时间流逝而确定性地流失。

构造再平衡对冲组合 (Rebalancing Portfolio)

为了定义 LVR，我们需要引入一个参照系：如果不做被动的 LP，而是主动管理仓位，结果会怎样？

我们构建一个“再平衡组合” \(V_{rebal}\)。该策略要求我们在外部市场（如 Binance 或合约市场）进行交易，使其在任意时刻 \(t\) 的持仓量精确等于 AMM 中的 \(x_t\)。
由于是在外部市场以公允价格主动交易，该组合不承担 AMM 的路径依赖亏损（即没有 Gamma 损耗项），其价值变化仅来源于资产价格的变动：

$$ dV_{rebal} = x_t dP_t $$

LVR 的最终解析解

LVR 被定义为“再平衡组合的收益”与“实际 LP 组合收益”之间的差额。这代表了 LP 因为被动成交（逆向选择）而相对于主动对冲者所损失的价值。

$$ dLVR_t = dV_{rebal} - dV_t $$

代入上述推导的表达式：

$$ dLVR_t = (x_t dP_t) - \left( x_t dP_t - \frac{\sigma^2}{8} V_t dt \right) $$

我们可以清晰地看到，包含 \(dW_t\) 的随机项 \(x_t dP_t\) 被完美抵消了。剩下的就是纯粹的、确定性的损失项：

$$ \boxed{dLVR_t = \frac{\sigma^2}{8} V_t dt} $$

对其在时间 \([0, T]\) 上积分，即得到累积 LVR：

$$ LVR_T = \int_0^T \frac{\sigma^2}{8} V_t dt $$

LVR 金融学意义

这一解析解公式 \(dLVR_t = \frac{\sigma^2}{8} V_t dt\) 将 LP 的亏损从模糊的“无常损失”坍缩为精确的“二阶损耗”，其金融学本质可归纳为以下三个维度：

物理本质：波动率税 (Volatility Tax) 与 Gamma 空头

公式中消除了随机项 \(dW_t\)，只剩下确定性的时间项 \(dt\)。这意味着：

• 做空 Gamma 的代价： 回顾泰勒展开中的 \(-\frac{1}{2} \Gamma \sigma^2 P^2\)，LVR 正是 LP 因为卖出 Gamma（凸性）而支付给市场的对价。无论价格涨跌，只要 \(\sigma > 0\)，LP 就在持续向套利者缴纳这笔“波动率税”。
• 路径依赖 (Path Dependence)： 与 IL “只看终点”的静态视角不同，LVR 是瞬时方差的积分。它像里程表一样记录了价格波动的总路程，揭示了震荡行情中 LP 本金被持续磨损的真相。

统计本质：信号与噪声

Alexander & Fritz 的研究深刻揭示了 LVR 与 IL 的统计对偶性：LVR 是 IL 的数学期望。

$$ \mathbb{E}[\text{IL}_T] \approx - \text{LVR}_T $$

• IL 是高方差的“噪声” (Ex-post)：单次路径中，运气好（价格回归）IL 可为 0，运气差（单边行情）则巨亏。
• LVR 是确定性的“信号” (Ex-ante)：LVR 剥离了价格方向的随机性，只保留了波动率的累积效应。它代表了 LP 策略的理论期望成本。

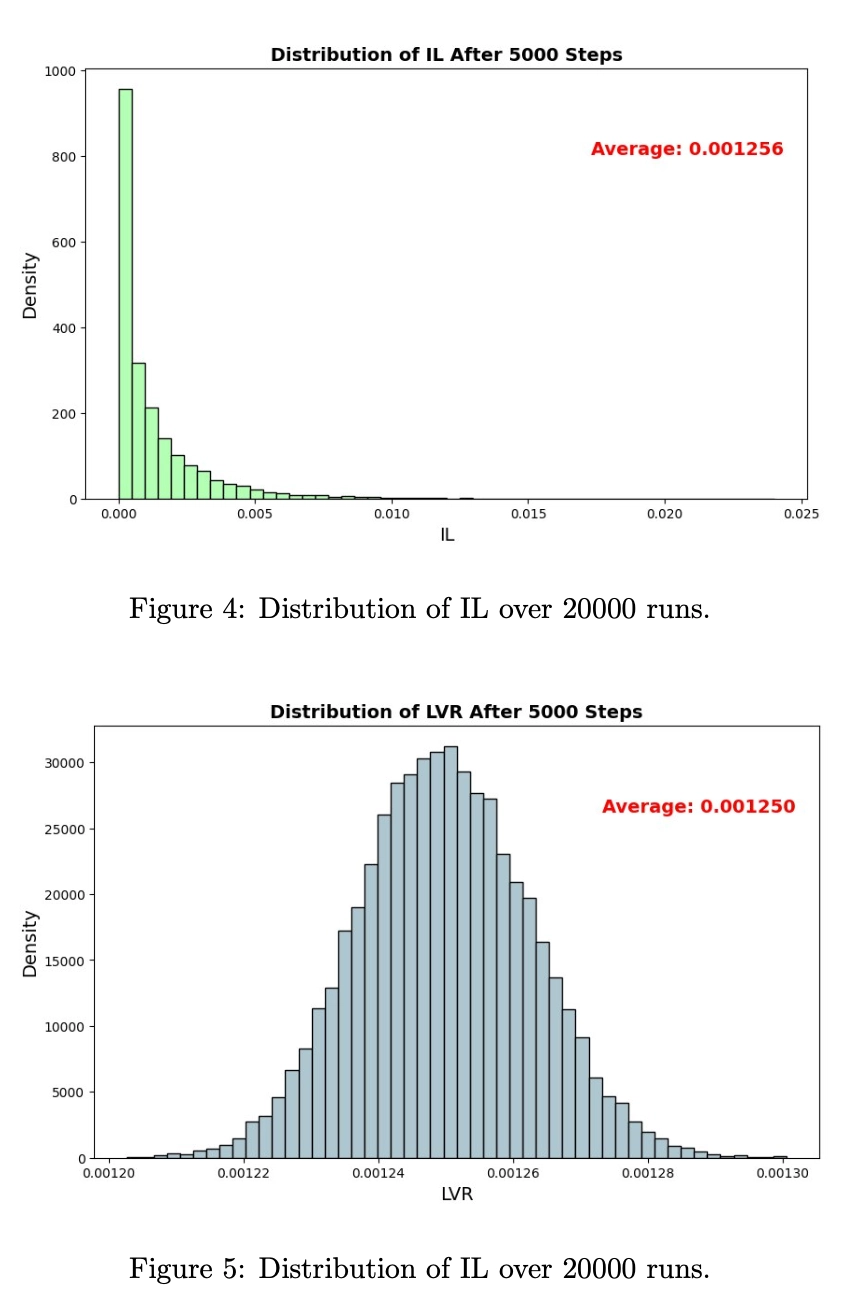
定价逻辑：期权映射

既然 \(LVR \propto \sigma^2 T\)，LP 的损耗就不再取决于预测价格涨跌，而取决于预测波动率。
这一结论直接导向了 Singh et al. 的核心发现：LVR 在数学上严格等同于“永久美式分期付款期权”的资金费 (Funding Fee)。

$$ \text{LVR Cost} \equiv \text{Option Premium} $$

这标志着 AMM 研究范式的根本转移：我们可以直接利用成熟期权市场的隐含波动率 (IV)，对链上流动性头寸进行精确定价。如果是做 LP，你本质上是在卖出一连串期限极短的跨式期权 (Short Straddle)。

总结与预告

从微观结构上看，AMM 的 LP 并不是在“被动理财”，而是在运行一个 做空跨式期权（Short Straddle） 的策略：我们向市场提供流动性（卖出期权），收取手续费（权利金），同时承担价格波动的风险（Gamma 损耗/LVR）。

判别 LP 是否赚钱的终极公式：

$$\text{Profit} = \text{Fees} - \text{LVR}$$

• Fees 取决于交易活跃度（噪音交易）。
• LVR 取决于市场波动率（\(\sigma^2\)）。

理解了 LVR，我们就理解了为什么高 APY 往往伴随着高亏损。在下一篇文章 【AMM量化深潜02】也就是做空波动率：Uniswap V3 的期权定价模型与 Greeks 中，我们将进一步利用这个数学框架，证明 Uniswap V3 的 LP 头寸本质上就是 一篮子奇异期权（Exotic Options），并利用期权定价模型对其进行精确定价和风控。

---

参考文献

• Alexander, Abe, and Lars Fritz. 2025. “Impermanent Loss and Loss-vs-Rebalancing I: Some Statistical Properties.” arXiv:2410.00854. Preprint, arXiv, May 14. https://doi.org/10.48550/arXiv.2410.00854.
• Cartea, Álvaro, Fayçal Drissi, and Marcello Monga. 2024. “Decentralised Finance and Automated Market Making: Predictable Loss and Optimal Liquidity Provision.” arXiv:2309.08431. Preprint, arXiv, June 13. https://doi.org/10.48550/arXiv.2309.08431.
• Lehar, Alfred, and Christine Parlour. 2025. “Decentralized Exchange: The Uniswap Automated Market Maker.” The Journal of Finance 80 (1): 321–74. https://doi.org/10.1111/jofi.13405.