利用相关性矩阵聚类构建统计套利组合：一种图聚类分析框架

统计套利策略的核心在于对资产价格暂时性偏离的识别和利用。传统方法如配对交易（Pairs Trading）已广为人知，但如何高效地扩展到大规模资产组合并保持稳健性，一直是研究难点。牛津大学研究团队近期在论文《Correlation Matrix Clustering for Statistical Arbitrage Portfolios》中提出了一种创新分析框架：利用图聚类算法（Graph Clustering）对股票残差收益的相关性矩阵进行聚类，并在每个簇内构建均值回归的统计套利组合。实证表明，该方法能产生年化收益超10%、夏普比率显著大于1的策略。

参考文献： Cartea, A., Cucuringu, M., & Jin, Q. (2023). Correlation Matrix Clustering for Statistical Arbitrage Portfolios. SSRN. https://ssrn.com/abstract=4560455

核心框架

该框架的核心流程简洁，主要包含两大阶段

1. 聚类相似股票 通过计算资产间的特定“相似性”（论文中主要基于残差收益相关性），再利用图聚类算法将股票划分为内部高度相关的群组（簇）。
2. 簇内套利 在识别出的每个簇内部署均值回归的统计套利组合进行交易。

构建相似性度量

论文中的相似性是基于历史收益率序列定义的。为了剥离市场整体波动的影响，聚焦股票自身特质性运动，论文首先计算了股票的市场残差收益（Market Residual Return）

$$ R_{i,t}^{res} = R_{i,t} - \beta_i R_{mkt,t} $$

其中

• \(R_{i,t}\)：股票 \(i\) 在时间 \(t\) 的原始收益。
• \(\beta_i\)：股票 \(i\) 的 CAPM Beta 系数（基于60天滚动窗口估计）。
• \(R_{mkt,t}\)：市场收益（以 SPY ETF 收益代理）。

接着，基于上述残差收益计算所有股票对间的 **相关性矩阵 \(\mathbf{C}\)**。矩阵元素 \(C_{ij}\) 表示股票 \(i\) 和 \(j\) 在回溯窗口 \(w\) 内残差收益的皮尔逊相关系数：

$$ C_{i,j} = \frac{\sum_{t=T-w}^{T-1} (R^{res}_{t,i} - \bar{R}^{res}_{i}) (R^{res}_{t,j} - \bar{R}^{res}_{j})}{(w-1) \sigma_i \sigma_j} $$

其中：

• \(\bar{R}^{res}_{i}\) ：股票 \(i\) 残差收益在 \(w\) 天窗口内的均值。
• \(\sigma_i\)：股票 \(i\) 残差收益在 \(w\) 天窗口内的标准差。
• \(w\)：回看窗口长度（论文中 \(w=5\) 天用于构建相关性矩阵）。

应用图聚类算法

相关性矩阵 \(\mathbf{C}\) 可被视为一个带权重的带符号网络（Signed Network）：股票是节点，相关系数是边的权重（可正可负）。

论文系统性地比较了五种能够处理负权重的图聚类算法：

1. SPONGE (Signed Positive Over Negative Generalized Eigenproblem) 通过广义特征值问题优化正负切割比，并引入正则化避免小簇。其数学表述涉及构造基于正相关 \(A^+\) 和负相关 \(A^-\) 的邻接矩阵分离出的拉普拉斯矩阵 \(L^+\) 和 \(L^-\)：

   $$ A = A^+ - A^-, \quad L^+ = D^+ - A^+, \quad L^- = D^- - A^- \quad \text{} $$

   最终求解广义特征值问题 \((L^+ + \tau^{-}D^-)v = \lambda (L^- + \tau^{+}D^+)v\)，取前 \(K\) 个最小广义特征向量进行后续的 k-means++ 聚类。

2. \(SPONGE_{sym}\) SPONGE 的对称归一化变体，使用对称归一化的拉普拉斯矩阵，对度数分布不均匀的网络更为鲁棒。其求解形式为

   $$ (L^{+}_{sym} + \tau^{-}I)v = \lambda (L^{-}_{sym} + \tau^{+}I)v $$

3. 谱聚类 (Spectral Clustering - Unsigned) 传统谱聚类方法，但需将相关性矩阵取绝对值 \(|C|\) 作为邻接矩阵（这会丢失负相关性信息），然后基于标准图拉普拉斯矩阵 \(L = D - |A|\) 进行聚类。

4. 有符号拉普拉斯 \(SignedLaplacian_{sym}\) 基于对称归一化的有符号拉普拉斯矩阵 \(\bar{L}_{sym} = I - \bar{D}^{-1/2}A\bar{D}^{-1/2}\) 进行聚类

5. 有符号拉普拉斯 \(SignedLaplacian_{rw}\) 基于随机游走归一化的有符号拉普拉斯矩阵 \(\bar{L}_{rw} = I - \bar{D}^{-1}A\) 进行聚类。

构建簇内统计套利组合

在划分出的每个股票簇 \(j\) 内部，基于过去 \(w\) 天的原始收益（论文实证表明组合仍能保持市场中性）构建交易策略

1. 计算簇平均收益

   $$ \bar{R}_{j,t} = \frac{1}{j_n} \sum_{i=1}^{j_n} R_{i,t} \quad \text{} $$

   (\(j_n\) 是簇 \(j\) 中的股票数量)。

2. 识别“前期赢家”与“前期输家”

   • Previous Winners 满足 \(\sum_{t=T-w}^{T-1} (R_{i,t} - \bar{R}_{j,t}) > p\) 的股票（论文中设 \(p=0\)，即近期累计收益高于簇平均的股票）。

   • Previous Losers 满足 \(\sum_{t=T-w}^{T-1} (R_{i,t} - \bar{R}_{j,t}) < -p\) 的股票（即近期累计收益低于簇平均的股票）。

3. 构建反向组合 做多 (Long) 所有 Previous Losers，同时做空 (Short) 所有 Previous Winners。

4. 分配权重 在每个簇内，保证组合初始名义价值为零（Dollar-Neutral），且多头总头寸与空头总头寸在金额上相等（例如，各为1单位）。如一个簇有2个Winners和4个Losers，则每个Winner分配 \(0.5\) 的空头权重，每个Loser分配 \(0.25\) 的多头权重。

5. 持有与再平衡 组合持有 \(\ell\) 天（论文中 \(\ell=3\) 天）。同时设置止盈阈值 \(q\)（论文中 \(q=5%\)），若组合在持有期内提前达到该收益，则立即触发再平衡流程。期满或触发止盈后，重新计算相关性矩阵、重新聚类、重新构建组合。

关键创新：基于相关性结构的图聚类

该框架没有采用直接对残差收益率向量进行传统聚类（如k-means）的路径，转而聚焦于相关性矩阵的图结构分析。这一设计源于对统计套利本质洞察：资产间的相对运动模式（协同性）比绝对收益水平更能定义“相似性”。本节讨论其主要优势

优化目标的转变

方法	目标函数	特点
K-means聚类	\(\min \sum_{k=1}^K \sum_{\mathbf{r}_i \in C_k} |\mathbf{r}_i - \boldsymbol{\mu}_k|^2\)	依赖欧氏距离，假设相似性=收益率幅度接近
图聚类	\(\max \frac{\sum_{i,j \in \text{same cluster}} C_{ij}^+}{\sum_{i,j} \in \text{different clusters}} |C_{ij}^-|\)	直接优化相关性结构，捕捉协同运动

处理负相关性的能力

图聚类显式优化正/负边切割（如SPONGE算法）

$$ (\mathbf{L}^+ + \tau^{-}\mathbf{D}^-) \mathbf{v} = \lambda (\mathbf{L}^{-} + \tau^{+}\mathbf{D}^+) \mathbf{v} $$

而K-means 无法区分负相关与弱相关 ，导致关键对冲机会丢失。

噪声鲁棒性

残差收益率向量 \(\mathbf{r}_i \in \mathbb{R}^T\) (T个时间点) 通常是高维且含噪的。直接对其应用k-means会面临：

• 维度灾难：当 \(T\)（时间长度）较大时，样本稀疏性导致距离度量失效。
• 噪声放大：收益率中的噪声会显著扭曲欧氏距离
• 时间平移不变性缺失：k-means无法捕捉延迟相关性（如股票A领先股票B变动）。

而图聚类通过两步抑制噪声：

1. 矩阵平均 相关性计算 \(C_{ij}\) 天然压制短期波动
2. 谱嵌入 对 \(\mathbf{C}\) 做特征分解 \(\mathbf{L} \mathbf{u} = \lambda \mathbf{D} \mathbf{u}\)，将节点映射到低维空间 \([u_1(i),…,u_K(i)] \downarrow\) 后再聚类。此过程压制了高频噪声，保留了稳健的拓扑结构。

关键创新：动态确定聚类数量 K

聚类数量 \(K\) 的选择对结果至关重要，该论文提供了一个动态确定 \(K\) 值的框架，摒弃了固定 \(K\) 的做法（如固定为30）。通过这些动态方法确定的 \(K\) 值在市场动荡时期（如2008年金融危机、2011年美债降级危机、2020年新冠疫情初期）会显著下降，这反映了市场风险结构或资产间联动模式的改变。

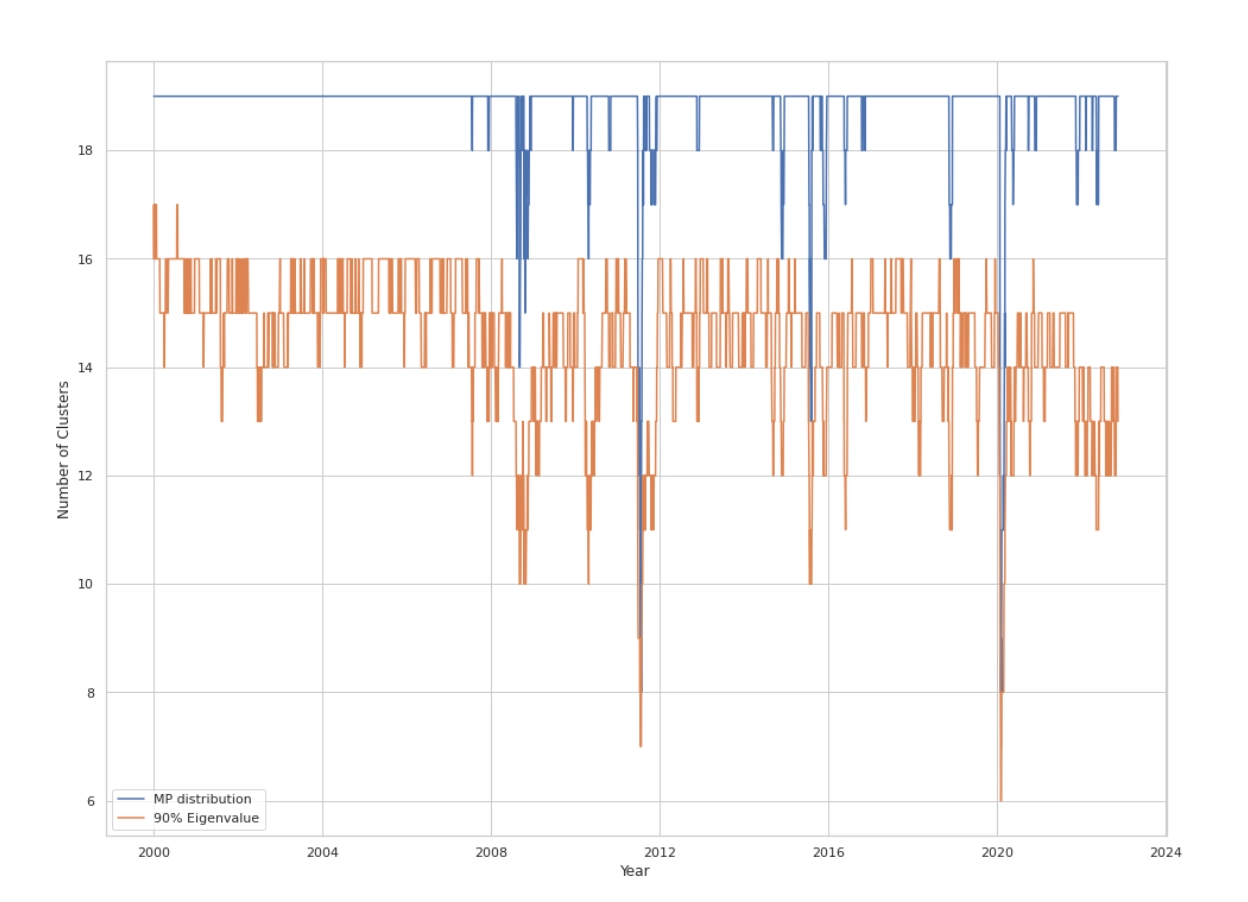
Marchenko-Pastur (MP) 分布法

基于随机矩阵理论 (RMT)：

• 计算残差收益矩阵 \(X\) (T天 \(\times\) N股) 的经验相关矩阵 \(C = \frac{1}{T}X^{T}X\)。

• Marchenko-Pastur 定律描述了在一定假设下（如 \(N, T \to \infty\), 且比率 \(\rho=N/T\) 固定时）\(C\) 的特征值 \(\lambda\) 的极限分布 \(f(\lambda)\)：

  $$ f(\lambda) = \begin{cases} \frac{\sqrt{(\lambda_{+}-\lambda)(\lambda-\lambda_{-})}}{2\pi\lambda\sigma^2\rho} & \text{for } \lambda \in [\lambda_{-}, \lambda_{+}] \\ 0 & \text{otherwise} \end{cases} \quad \text{} $$

  其中 \(\lambda_{\pm} = \sigma^2(1 \pm \sqrt{\rho})^2\)。若收益已标准化使 \(\sigma^2=1\)，则 \(\lambda_{\pm} = (1 \pm \sqrt{\rho})^2\)。

• \(K\) 被设定为经验相关矩阵 \(C\) 中大于理论上界 \(\lambda_{+}\) 的特征值的数量。这些“离群”的特征值被认为对应于市场中显著的、非随机的结构信息或主导因子。

累积方差解释法 (90% Eigen)

• 将相关矩阵 \(C\) 的特征值按降序排列 \(\lambda_1 \ge \lambda_2 \ge … \ge \lambda_N\)。

• \(K\) 被设定为满足 \(\frac{\sum_{i=1}^{k} \lambda_i}{\sum_{i=1}^{N} \lambda_i} \ge P\) 的最小 \(k\) 值（论文中采用 \(P=0.9\), 即解释90%的总方差）。

实证结果：强劲且稳健的绩效

该研究使用CRSP数据库中2000年至2022年期间，每日市值排名前25%的美股（约600只/天）进行回测。

绩效

Model	MP AR	MP SR	MP ST	90% Eigen AR	90% Eigen SR	90% Eigen ST	Fixed K AR	Fixed K SR	Fixed K ST
SPONGE	10.99	1.02	1.81	11.90	1.07	1.89	10.21	1.01	1.80
SPONGE\(_{sym}\)	12.05	1.11	2.01	12.20	1.10	2.01	10.40	1.03	1.80
Spec	10.96	1.03	1.82	10.84	0.98	1.75	10.03	0.99	1.72
Lap\(_{sym}\)	11.19	0.91	1.60	11.24	0.88	1.55	11.10	0.97	1.66
Lap\(_{rw}\)	10.38	0.85	1.47	11.26	0.90	1.56	10.95	0.96	1.64
FF12	-	-	-	-	-	-	10.13	1.08	1.90
SPY	-	-	-	-	-	-	6.59	0.32	0.50

• 主要绩效指标 年化收益 (AR)、夏普比率 (SR, 假定无风险利率为0)、索提诺比率 (ST)。

• 基准策略 SPY ETF (市场基准)；FF12 (在Fama-French 12个行业分类内部，采用与聚类策略相同的簇内均值回归逻辑构建的组合，即将行业视为“簇”)。

• 所有基于聚类的套利策略，无论采用何种 \(K\) 值选择方法，其年化收益普遍超过10%，显著优于市场基准SPY (约6.59%)。

• 在不同聚类算法中，\(SPONGE_{sym}\) 整体表现最佳，尤其在动态 \(K\) 值选择下，其年化收益可达12%以上，夏普比率超过1.1，索提诺比率接近或超过2.0。

• 动态确定 \(K\) 值的方法均略优于固定 \(K=30\) 所得结果，表明动态方法对市场具有一定的自适应能力。

市场中性验证

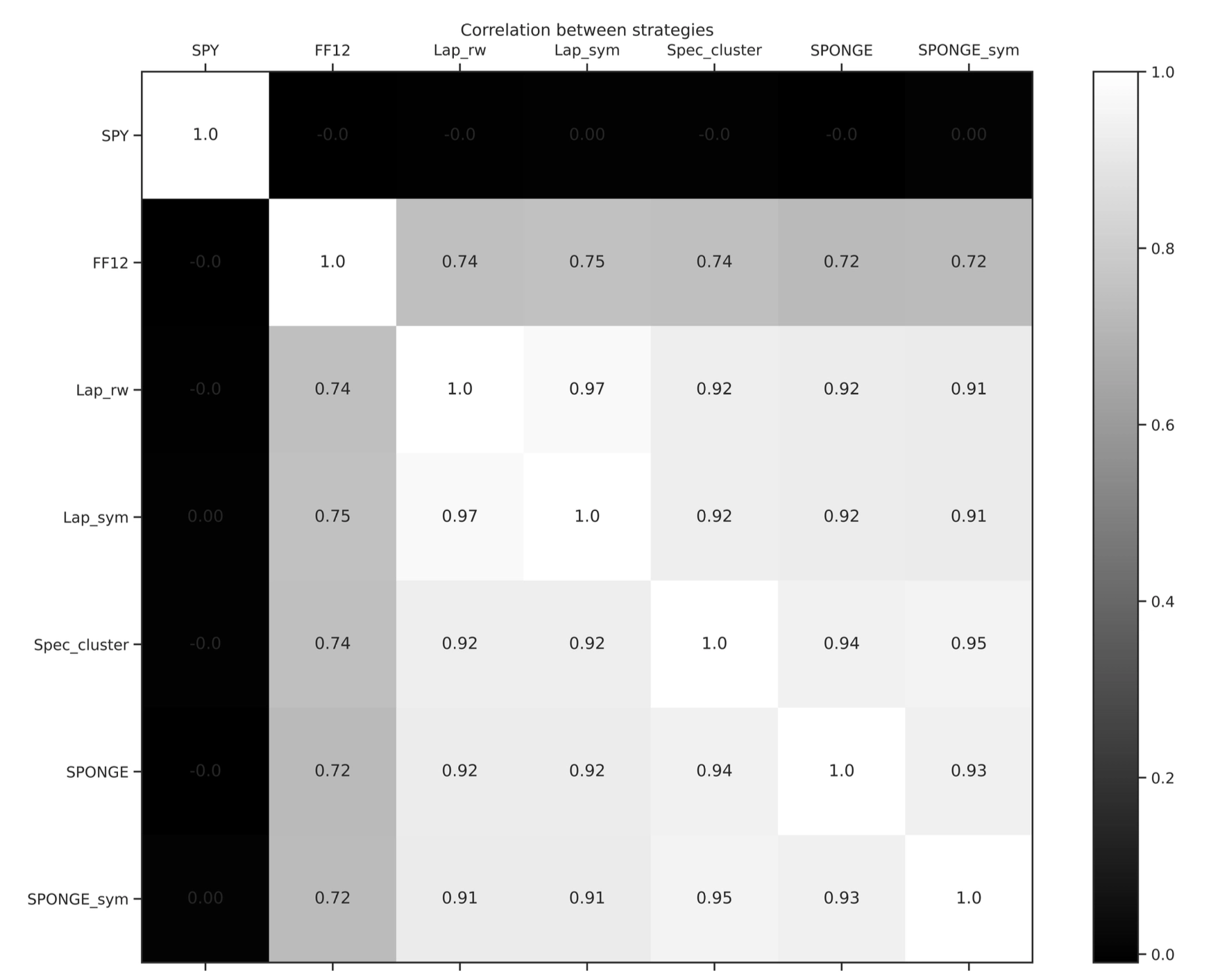
• 策略收益相关性矩阵显示，所有统计套利策略的收益序列与SPY ETF收益序列的相关系数均接近于零。这有力地证实了这些策略的市场中性特性。
• 不同图聚类算法驱动的策略之间收益相关性非常高，表明它们捕捉到了相似的均值回归模式。

超越行业分类的效应

• SPONGE算法发现的簇仅部分与特定行业（如公用事业、能源、商业设备、医疗保健）存在较大重合，同时存在许多包含来自多个不同行业股票的大型簇。
  

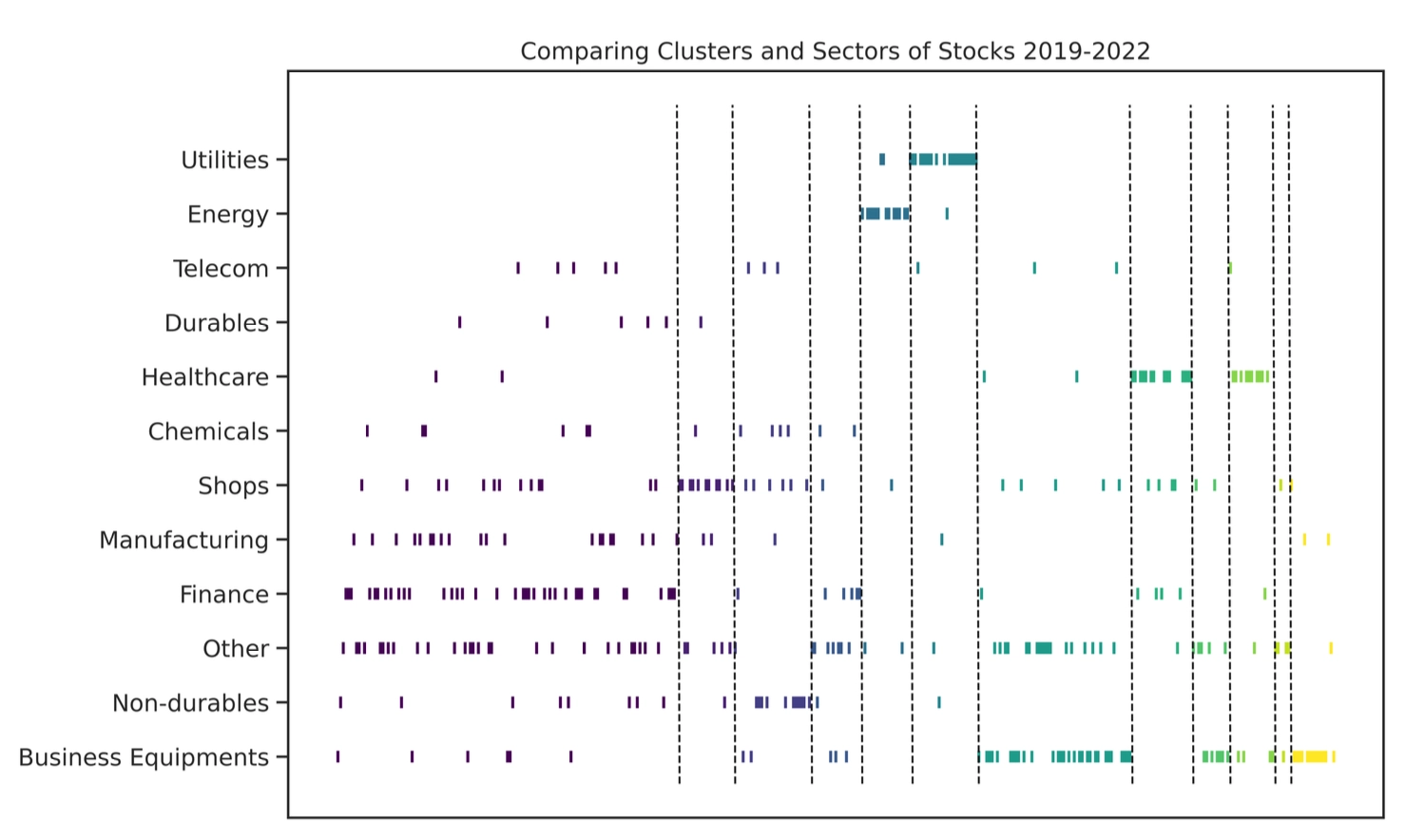
• 论文使用调整兰德指数 (Adjusted Rand Index, ARI) 量化了聚类结果与FF12行业标签的相似性。所有聚类算法得出的簇划分与行业分类的ARI均低于15%。

• 同时，各聚类策略的收益与FF12行业策略的收益相关系数也相对较低。

• 这些证据共同表明，该框架下策略的超额收益并不能完全被传统行业内的均值回归效应所解释。聚类方法成功发掘了跨行业的、更新颖的均值回归获利机会。

结论

该论文提出的基于相关性矩阵图聚类的统计套利框架，展现出多方面优势

1. 高效的资产分组机制 图聚类算法，特别是SPONGE系列，能够有效地从高维相关性数据中识别出具有相似残差收益模式的股票群组。
2. 显著的盈利能力 在识别出的簇内应用简单的“做多输家/做空赢家”反向交易逻辑，即可实现年化超10%的收益，且风险调整后收益指标（夏普比率 > 1, 索提诺比率 > 1.8）表现突出。
3. 可靠的市场中性 通过对残差收益进行建模并构建美元中性组合，策略收益与市场基准（SPY）的相关性接近零，表现出良好的对冲效果。
4. 超越传统行业的Alpha来源 策略所捕捉的均值回归模式与基于固定行业划分的模式存在显著差异，证明其发掘了新的、独立的Alpha来源。
5. 动态且鲁棒的框架设计 基于随机矩阵理论动态调整聚类数量 \(K\) 的机制，使得整个框架对 \(K\) 的具体选择以及所用聚类算法的类型均表现出较好的稳健性。

启示与展望——拓展“相似性”的维度

该研究为量化投资提供了强大的实践框架，其核心思想——利用数据驱动的方法识别资产间的“相似性”结构，并在此基础上构建交易策略——具有广泛的适用性和巨大的发展潜力。特别是在定义和度量资产“相似性”方面，存在丰富的拓展方向

• “残差收益”定义的拓展性
  论文主要采用CAPM模型剥离市场因素得到残差收益。然而，获取“特质性”或“残差”收益的方法本身极具灵活性。例如，可以采用主成分分析 (PCA) 等纯粹的统计方法从原始收益率中识别并剔除市场共性风险（即由主成分代表的风险因子），从而获得不同视角下的残差收益序列。这些序列可能捕捉到与CAPM不同的资产特有动态。

• “相似性”度量与自定义嵌入 (Custom Embeddings) 的引入

  • 当前框架以残差收益的相关性矩阵作为聚类算法的输入。未来的研究可以进一步拓展“相似性”的内涵。可以不局限于简单的线性相关性，而是借鉴现代因子投资与机器学习（尤其是深度学习）的思路，引入更丰富的 自定义资产嵌入（Custom Asset Embeddings） 来表征股票。
  • 例如，可以综合利用股票的基本面数据（如财报指标）、另类数据（如新闻文本情感分析、专利数据、供应链关系、分析师研报观点）、高频交易数据特征，通过深度学习模型（如自编码器、Transformer、图神经网络等）学习每只股票的低维稠密向量表征（Embedding）。
  • 这些学习到的嵌入向量能够捕捉到更复杂、更深层次的资产特性与关联模式。随后，可以基于这些嵌入向量计算股票间的相似度或距离（如余弦相似度、欧氏距离或其他更复杂的核函数），并以此构建新的“相似性矩阵”作为图聚类算法的输入。
  • 这种方法为从更多元、更本质的维度（例如，基于相似的商业模式、相似的风险暴露、相似的成长逻辑、相似的投资者关注度模式，或产业链上下游等经济关联）来发现和定义资产簇提供了广阔的探索空间，有望捕捉到传统相关性分析难以触及的套利机会。

• 框架其他部分的延伸探索

  • 聚类算法的持续创新 可以继续探索和评估更新的、更复杂的图聚类或社群发现算法，特别是那些能处理动态网络、异构信息或提供更佳可解释性的方法。
  • 簇内组合构建的优化 除了简单的反向均值回归策略，还可以研究在簇内应用更精细化的组合优化技术，例如基于协整关系、风险平价模型，或者结合簇内资产的其他特性（如动量、波动率等）进行差异化加权。
  • 跨资产与高频应用 正如论文作者所建议，可以将此框架尝试应用于其他资产类别（如加密货币、外汇、大宗商品等）或跨资产的相关性矩阵分析，以及在更高频率的数据（如分钟级甚至tick级数据）上挖掘极短期的均值回归机会。

总之，这项工作不仅为统计套利策略的研发提供了一套系统化、可操作性强的分析框架和工具集，也为评估和应用各类图聚类算法于金融市场分析设立了新的基准和参考。其对资产“相似性”的灵活定义与数据驱动的挖掘方式，预示着未来在这一方向上存在着持续创新的巨大潜力。