衡量序列相关性的三个指标——从线性到非线性

本文介绍了三种度量变量相关性的指标：Pearson相关系数、Spearman相关系数和Chatterjee相关系数，最后一种可以简便地衡量非线性相关关系。

Pearson相关系数用于衡量随机变量X，Y之间的线性相关性，它的定义是X,Y的协方差比上各自的标准差

$$ \rho_{X,Y} = \frac{cov(X,Y)}{\sigma_X\sigma_Y}=\frac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X\sigma_Y} $$

协方差度量了X，Y之间偏移各自均值的关联关系，不会受到平移的影响。而除以标准差保证了不受尺度放缩的影响。Pearson相关系数的值域是\([-1,1]\)，当取值大于0时表示正相关，反之为负相关，且绝对值越大线性关系越强，等于0时表示没有线性相关关系。

Spearman相关系数又被称为秩相关系数，它先将X，Y转化为等级（排名）序列R(X),R(Y)，然后计算Pearson相关系数。

$$ r_s=\rho_{R(X),R(Y)} $$

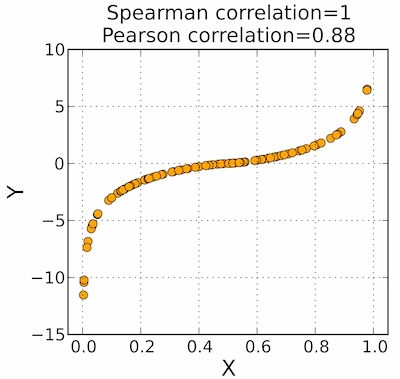
这样做的好处是一是避免极端值的影响，二是不要求原始值线性相关。如下三张对比图很好地对比了两者

• 图1中秩相关系数准确地反映了Y完全随X变化
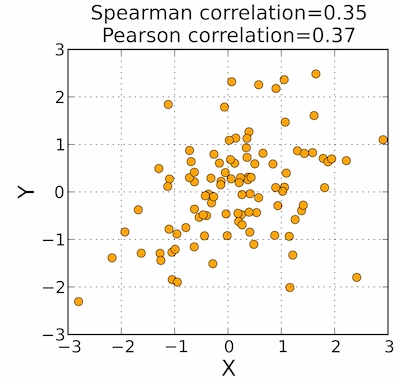
• 图2中两者类似
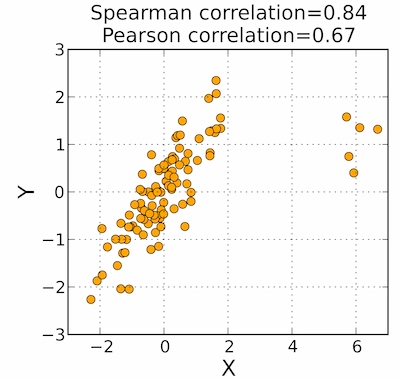
• 图3中秩相关系数没有受离群值的影响，反映了X，Y高度相关，而皮尔逊相关系数只有0.67

上述两种相关系数只能描述线性相关性，面对如\(y=x^2\)之类的非线性函数无能为力。因此人们又提出了非线性相关分析算法最大互信息系数MIC，但计算复杂度上升了几个数量级，效果也难尽人意。人们想要的其实是这么一个指标

1. 要像Pearson相关系数或Spearman相关系数那样简单
2. 能够始终准确估计变量间依赖程度的某种简单且可解释的度量，这个度量在且仅在变量独立时为0，而在且仅在一个是另一个的可测函数时为1
3. 在独立假设下具备简单的渐近理论，类似于经典系数

有这么好的事吗？还真有！本文要介绍的第三个指标是2019年被提出的Chatterjee相关系数（CCC）。假设 \((X_1, Y_1), \ldots, (X_n, Y_n)\) 独立同分布，其中 \(n \geq 2\)，且 \(X_i\) 和 \(Y_i\) 没有任何相等的值。将数据重新排列为 \((X(1), Y(1)), \ldots, (X(n), Y(n))\)，使得 \(X(1) \leq \ldots \leq X(n)\)。设 \(r_i\) 是 \(Y(i)\) 的等级，即 \(Y(j) \leq Y(i)\) 的 \(j\) 的数量。新的相关系数定义如下：

$$ \xi_{n}(X, Y):=1-\frac{3 \sum_{i=1}^{n-1}\left|r_{i+1}-r_{i}\right|}{n^{2}-1} $$

直观的理解是，Chatterjee相关系数衡量顺序排列\(X_i\)后，相邻的\(Y_i\)是否相近。理论证明详见原文[1]. 值得注意的是，该指标并非对称，且是作者有意为之，计算相关性时需要计算两次取最大值。指标效果如下图所示，相比皮尔逊相关系数，能够识别非线性相关性，但对线性相关情况有些低估。

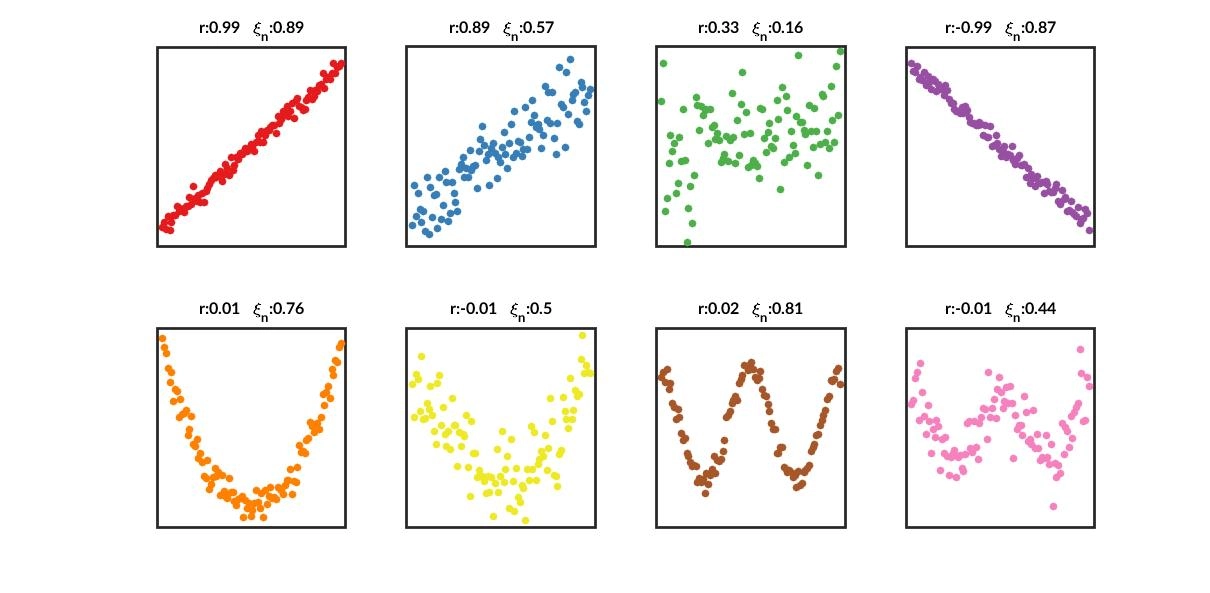
下面给出python实现

import numpy as np

def cal_maxCCC(X, Y) -> float:
    def _CCC(X, Y):
        Y_sort_by_X = Y[np.argsort(X)]
        Y_ranks = np.argsort(np.argsort(Y_sort_by_X))
        ccc = 1 - 3 * np.abs(np.diff(Y_ranks)).sum() / (len(Y) ** 2 - 1)
        return ccc

    return max(_CCC(X, Y), _CCC(Y, X))

[1.] Chatterjee, Sourav. 2021. 《A New Coefficient of Correlation》. Journal of the American Statistical Association 116 (536): 2009–22. https://doi.org/10.1080/01621459.2020.1758115.