数字货币永续合约资金费率套利策略

本策略通过资金费率机制和质押收益捕捉数字货币市场中的低风险套利机会。

策略原理

资金费率

机制

交易所建立了资金费用机制确保永续合约的价格反映交易标的市场变化。该机制促使多仓与空仓持有者之间定期进行现金流交换，使永续合约的价格向指数价格收敛。当资金费率为正数时，多仓位持有者支付资金费用给空仓持有者；相反，当资金费率为负数时，空仓持有者支付资金费用给多仓持有者。资金费用每8小时结算一次。

在币本位合约中，持仓仓位价值 = 合约张数 × 合约面值 × 合约乘数 / 标记价格

例：用户持有 100 张 ETHUSD 永续合约空仓仓位，当前标记价为 4,000 USD ，合约面值为 10 USD，资金费率为 0.1%。

持仓仓位价值 = 100 × 10 × 1 / 4,000 = 0.25 ETH

资金费用 = 0.25 × 0.1% = +0.00025 ETH

资金费用由平台直接发放到用户的交易账户中。

收益分析

资金费率来源包括固定利率和市场溢价，两者共同决定了长期正收益的可能性。 如币安使用固定利率，并假设持有约当现金获得的利息高于持有等值BTC 获得的利息。币安合约利率预设为每日0.03% (资金计算每8小时执行一次，因此每个资金间隔利率为0.01％)，年化收益率约为11%。溢价指数(P) = [Max(0,冲击买方出价-价格指数) - Max(0,价格指数-冲击卖方出价)] / 价格指数

这两个因素导致累计资金费用通常是正值：

• 基础利率为正
• 散户倾向于在合约中加杠杆做多，而不是做空。绝大多数合约交易者开的第一单是做多，因为做多赚钱更符合直觉，同时价格上涨有无限的想象空间，做空收益则是有限的。

从各大交易所历史数据上看，大部分币种的资金费率在大多数时间内呈正值，且有较强的延续性。

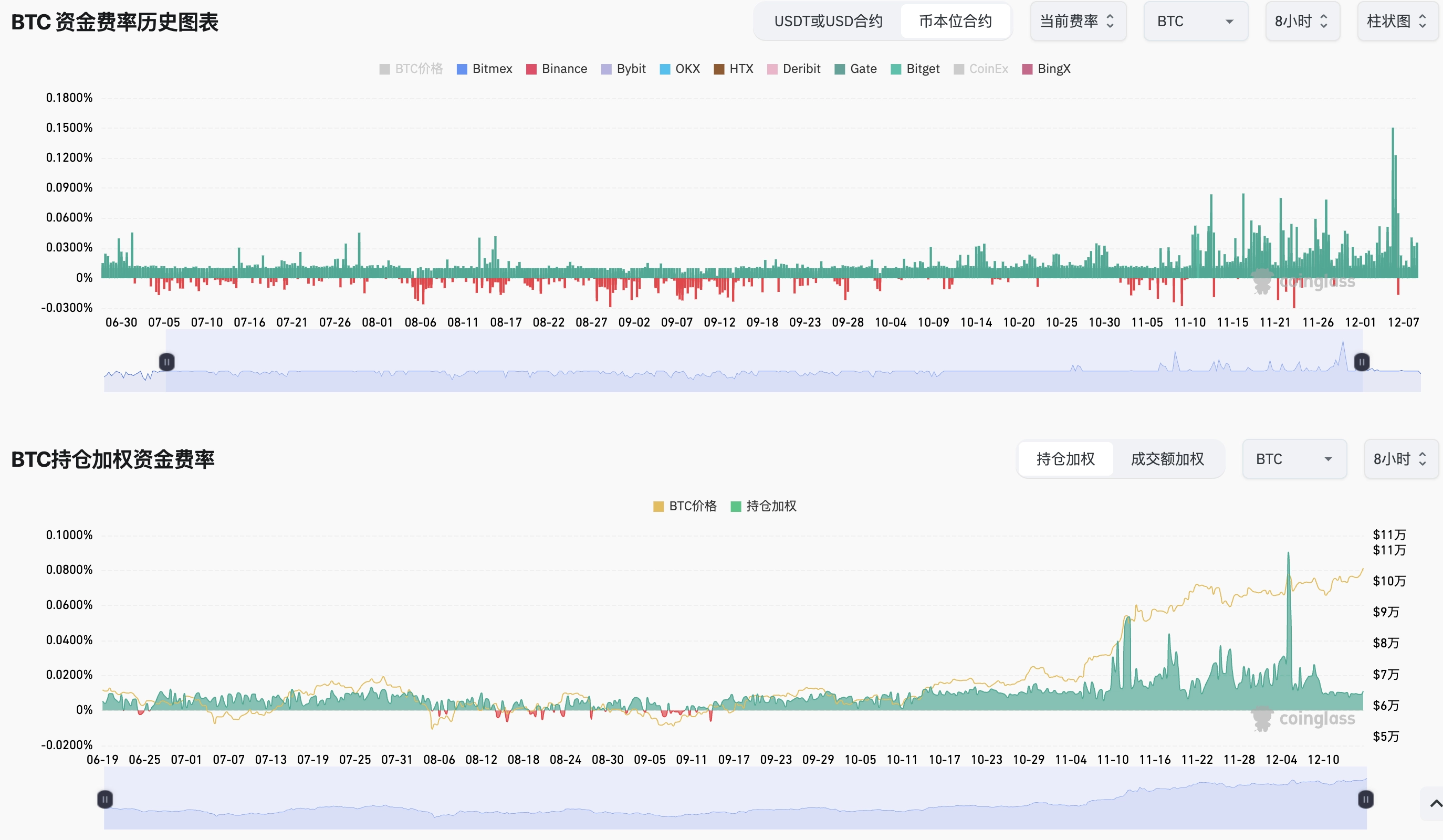
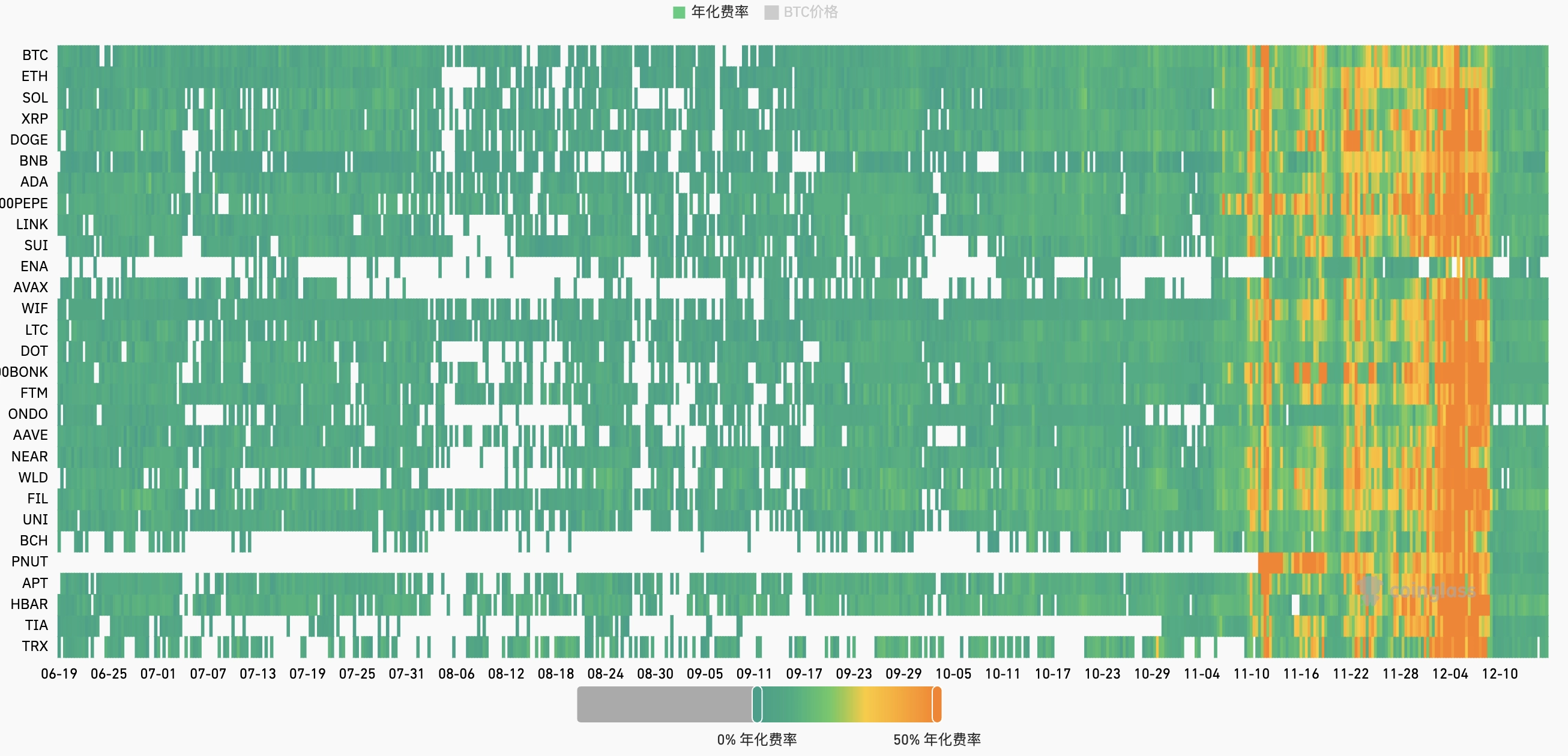
币本位套利

获取资金费率的最优方式是卖出币本位永续合约。传统套利同时持有现货、U本位永续合约进行风险对冲，遗留了两个问题：

• 资金利用率低。 如75%资金购买现货，25%作为合约保证金3x杠杆，收益率有折损。
• 爆仓风险。 即便使用1x杠杆，仍有可能爆仓。

币本位合约又称反向合约，直接使用虚拟币作为保证金。策略在买入现货后，用现货作为保证金开空头仓位，资金利用率是100%。同时，如果币价上涨，保证金价值同步上升，币本位机制下1x杠杆的空头合约没有爆仓风险。

永续合约套利的收益来源由资金费率和价差组成。

• 资金费率 上文已分析过，资金费率长期来看年化约15%左右，牛市时期约30%-50%。在策略执行过程中，会预测、选取短期内高费率品种进行轮动，预计年化20%+。
• 价差 也会对收益造成短期影响。（由于期现套利者的存在价差通常在0.1%以内）
  • 开仓时，会将价差作为手续费纳入考量。
  • 开仓后，溢价上升。此时合约出现浮亏，但溢价上升导致资金费率上升，惩罚多头奖励空头，对长期持有是有利的。
  • 开仓后，溢价下降。此时可以从价差中获利，考虑离场切换套利对。

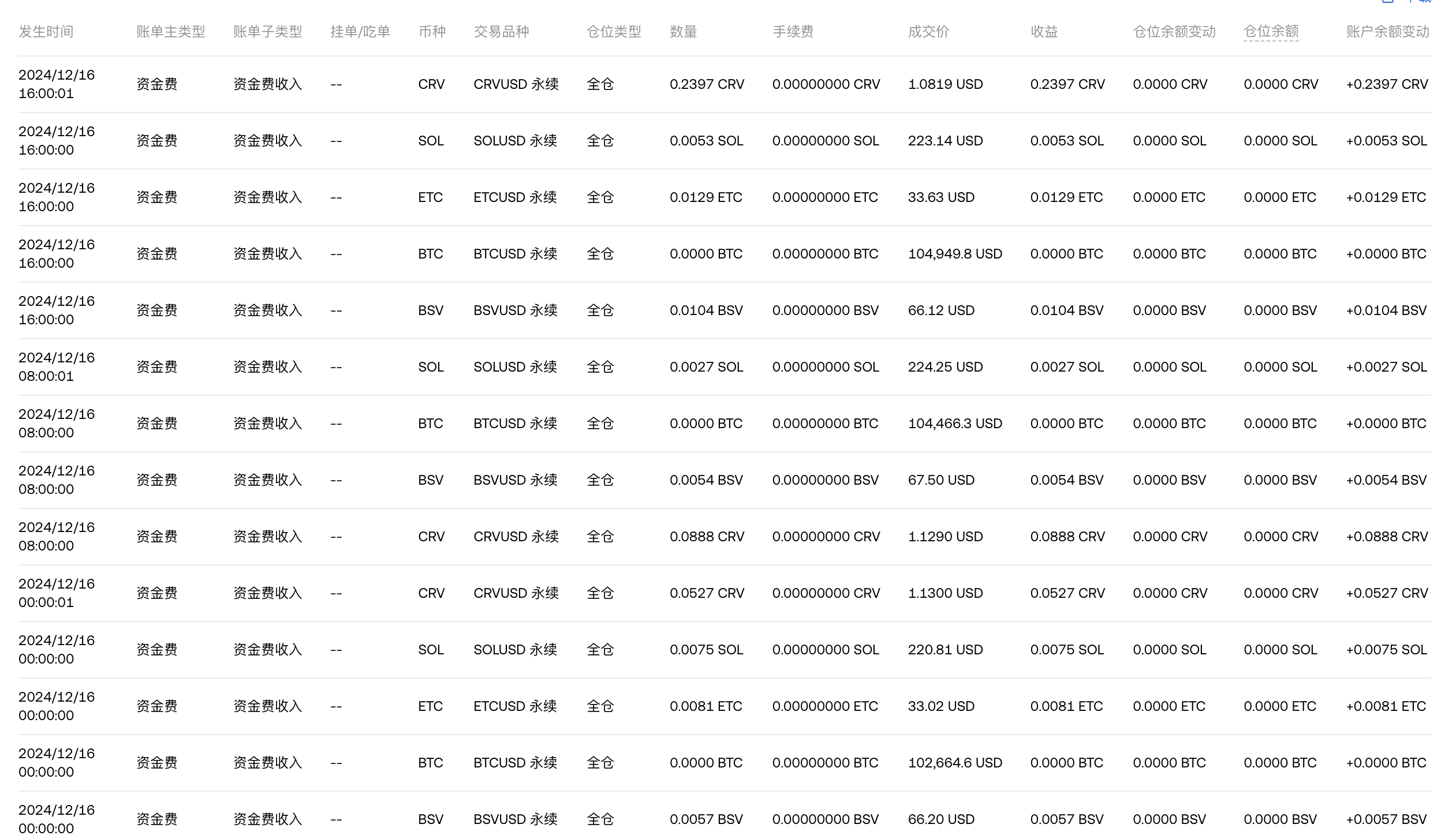
质押收益

对于部分特殊代币(ETH, SOL)，可以在不增加杠杆的情况下，通过在区块链上质押（staking）增厚收益。

质押代币可以获取额外收益，如当前$SOL质押年化收益为11%+。质押SOL可以获得收益的原因与区块链网络的权益证明（Proof of Stake, PoS）共识机制相关。质押 SOL 时，这些代币被委托给验证者节点，验证者使用这些代币参与网络共识，打包区块并验证交易。作为回报，网络会给予验证者区块奖励和交易费用分成，其中主要是通胀奖励，以及交易者为加速交易支付的小费，在交易活跃时收益更高。

质押原生代币不会导致杠杆率的上升，依然没有爆仓风险。原理是通过交易所质押资产，平台会发放流动性代币作为质押证明，如OKSOL对应质押后的SOL。OKSOL可以1:1兑换为SOL，两者价值几乎一致。因此，可以将OKSOL转入交易账户作为跨币种保证金，替代SOL现货。

量化实现

低风险套利通常可以由手工操作完成，自动化策略则可以实现更智能的品种轮动，更精细化的交易执行。

品种轮动的监督学习框架

我们假设：

1. 手续费 \(c_i\) 是固定的，仅在开仓时支付一次，与持仓期无关。
2. 借鉴强化学习的奖励函数，每个币种的目标是预测未来资金费率的加权求和（即折现的累计资金费率收益）。

对于币种 \(i\)，定义未来资金费率的加权求和为：

$$ G_i = \sum_{k=1}^T \gamma^{k-1} \hat{r}_i^{t+k} - c_i $$

其中：

• \(\hat{r}_i^{t+k}\)：未来第 \(k\) 期的资金费率
• \(\gamma \in (0, 1]\)：折扣因子，衡量未来收益的权重。
• \(c_i\)：开仓成本，包括手续费、价格冲击以及价差。

策略的核心是对每个币种预测 \(G_i\)。可以通过机器学习或时间序列建模来直接估计 \(G_i\)，具体步骤如下：

每个币种的数据集包括历史资金费率序列 \([r_i^{t-k}, \dots, r_i^t]\) 和目标值 \(\hat{r}_i^{t+k}\)。

特征设计：

• 历史资金费率 \([r_i^{t-k}, \dots, r_i^t]\)。
• 市场行情特征（如价格波动、成交量）。
• 技术指标（如移动平均、波动率）。

使用机器学习模型（如 LSTM、Transformer 或传统回归模型）预测资金费率的加权求和 \(G_i\)：

$$ \hat{G}_i = f_\theta(s_i) $$

其中：

• \(s_i = {r_i^{t-k}, \dots, r_i^t, \text{其他特征}}\)：输入特征。
• \(f_\theta\)：预测模型，输出币种 \(i\) 的累计收益估计值。

目标是最小化预测误差：

$$ \mathcal{L} = \frac{1}{N} \sum_{i=1}^N \left( \hat{G}_i - G_i \right)^2 $$

每个时间步 \(t\)，根据所有币种的 \(\hat{G}_i\) 选择收益最大的币种开空：

$$ i^* = \arg\max_i \hat{G}_i $$

这一方法高效、直观且易于实现，同时保留了收益最大化的核心目标。

交易执行

上述的套利逻辑需要先后完成在现货与合约的交易，手动下单容易有延迟导致风险暴露。从节约交易手续费的角度来说，应该先在合约中挂单，成交后立刻市价卖出现货，保持市场暴露中性。换仓时，策略可以在交易对构成的图结构中搜索最优执行路径，例如BTC->ETH->SOL, BTC->USDT->SOL。