Quant4.0（一）量化投资简介，从1.0到4.0

近年来，量化投资产业在国内蓬勃发展，成为讨论二级市场时绕不开的话题，或被神话，或人人喊打。那么，究竟什么是量化投资(Quantitative Investment)？有哪些量化策略，量化策略一定赚钱吗？构建量化策略有哪些基本原则？本文介绍了量化投资的基本概念、前世今生，并展望其未来发展模式。

本文是对论文Quant 4.0: Engineering Quantitative Investment with Automated, Explainable and Knowledge-driven Artificial Intelligence的部分翻译，有删改。原文地址

Quant4.0（一）量化投资简介，从1.0到4.0

Quant4.0（二）自动化AI与量化投研

Quant4.0（三）可解释AI、知识驱动AI与量化投研

Quant4.0（四）系统整合与简化版量化多因子系统设计

财富管理与量化

财富管理行业是全球经济最大的部门之一。根据波士顿咨询集团（BCG）的一份全球财富报告[1]，全球金融财富的规模从2016年的188.6万亿美元增长到2021年的274.4万亿美元，几乎是2021年全球名义国内生产总值的三倍。此外，该公司预测这一数字将在2026年增至355万亿美元。随着数字经济、大数据和人工智能的迅猛发展，越来越多的新技术应用于财富管理行业，导致了一种称为“投资工程”的金融科技/工程的分支[3]。投资研究、交易执行和风险管理的流程正在变得系统化、自动化和智能化，这一理念在量化的最近演变中得到了实践。

作为金融市场和财富管理行业中重要的参与者群体，如今量化通过严格的数学和统计建模技术、机器学习技术以及算法交易技术，量化投资在金融市场中发现资产定价异常，并从随后的套利或投资机会中获利。与传统的基本面和技术投资相比，量化投资具有许多优势。

• 首先，可以在真正交易开始之前使用基于历史数据的回测实验预先检查和评估量化策略的表现。
• 其次，量化交易在以最佳价格报价订单方面具有速度优势。
• 第三，它消除了决策过程中人类情感的负面影响。最后，在数据分析方面，量化研究在对金融市场和行业信息的深度、广度和多样性上具有显著优势。

在过去的30年中，全球金融交易市场广泛应用了信息基础设施和计算机技术。如今，每秒生成大量的金融数据，执行数百万订单，导致量化行业迅速增长。以美国股票市场为例，超过60%的总交易量来自计算机交易算法而非人类交易者。

量化策略

量化策略是一种基于预定义规则或经过训练的模型做出交易决策的系统，通常是量化基金的核心智能资产。

量化策略的组成部分

标准的量化策略包含一系列组成部分，如投资工具、交易频率、交易模式、策略类型和数据类型。

• 投资工具指定策略将哪些金融工具纳入投资范围。流行的候选工具包括股票、交易所交易基金（ETF）、债券、外汇、可转债以及更复杂的金融衍生品，如期货、期权、掉期和远期[6]。投资策略可以交易单一类型的工具（例如，用于交易ETF的策略）或多种类型的工具（例如，一个同时做多股票和做空指数期货以消除市场风险的alpha对冲策略）。
• 交易频率指定如何持有投资组合中的资产以及交易的频率。通常，高频交易在几分钟或几秒钟内持有仓位，而低频交易可能在几个月或几年内持有资产。与高频交易和低频交易相比，持有期限的显著差异导致了策略设计上的非常不同的考虑。例如，对于高频交易，资产容量限制和交易成本是重大问题，而对于低频交易，我们应该仔细思考如何控制回撤风险[7]。
• 模型类型表征如何正式对交易问题建模。示例包括横截面交易、时间序列交易和事件驱动交易[7]。横截面交易通常在股票选择中使用，其中所有股票在量化策略中，横截面交易是常见的，投资范围中的所有股票按照模型预测的未来回报的分数进行排名，投资组合经理可以做多得分最高的股票，并做空得分最低的股票。与时间序列交易不同，事件驱动交易的时间间隔在时间上不均匀分布，而投资决策和交易执行是由事件发生触发的。
• 交易类型是我们设计策略的一系列思考模板。示例包括动量交易[8]、均值回归交易[9]、套利交易[10]、对冲[11]、做市[12]等。通过利用这些策略类型，交易者可以从金融市场的不同方面探索利润机会。具体而言，动量交易假设价格趋势在接下来的时间窗口内是可持续的，并按照这个趋势方向进行交易。相反，均值回归交易则打赌价格趋势将在近期朝着相反方向移动，并购入相反的仓位。对冲是购买一种资产，以减少另一种资产的损失风险。套利是在不同市场同时做多和做空相同资产，或者是在一对高度相关的资产中做多和做空，以从价格差异的收敛中获利。做市是提供流动性的交易，对可交易资产报出买入和卖出价格，希望通过买卖价差获利。
• 数据类型表示策略中使用的是哪种类型的数据。典型的数据类型包括行情数据、限价订单簿[13]、新闻数据、财务报表、分析师报告，以及情感数据、位置数据、卫星图像等替代数据。在策略开发过程中，策略研究人员必须考虑他们拥有哪些数据以及在策略开发过程中需要哪些数据。例如，限价订单簿流通常用于构建高频交易策略，而新闻数据在事件驱动策略中更常用。

资产管理的基本原则

类似于学习能量守恒法则有助于避免陷入永动机的陷阱，学习一些资产管理的基本原则对于摆脱策略开发中的一些常见陷阱是有益的。

主动管理的基本法则

第一个原则是由理查德·格林诺德（Richard Grinold）和罗纳德·卡恩（Ronald Kahn）提出的主动管理的基本法则[15]。该法则表明主动投资经理（或等效的量化模型）的表现取决于投资技能的质量以及投资机会数量。这一法则可以用数学方式表达为：

$$\text{IR} = \text{IC} \times \sqrt{\text{BR}},$$

其中：

• \(\text{IR}\) 表示信息比率，衡量了主动管理的效果；
• \(\text{IC}\) 表示信息系数，即模型对未来收益的预测准确性；
• \(\text{BR}\) 表示投资机会的频率与观察时间窗口之比。

这一公式强调了主动管理的关键在于投资技能的质量和投资机会的频率。如果一个投资经理能够更准确地预测未来收益（更高的信息系数），并且有更多的投资机会，那么其主动管理的效果将更好。这对于量化策略的开发者来说是一个重要的原则，因为它指导着他们在提高模型预测准确性和寻找更多投资机会方面的努力。评估投资质量时，广度表示一年中独立投资决策的数量，而IR是投资组合收益超过基准收益与收益波动率之比，衡量资产管理的绩效。从数学上来说，主动管理的基本法则可以被视为数学统计中中心极限定理的应用[16]。在实际应用这一法则时，我们必须注意IC和广度通常不是独立的。例如，给定一个策略，我们可以通过放宽交易信号的阈值来增加其广度，但这样一来，IC可能会减小，因为更多的假阳性噪声被引入到我们的决策中。因此，一个好的策略应该在这两个耦合变量之间找到一个最佳的权衡。图4a展示了各种流行策略在IC和广度上的分布，以及它们对应的IR绩效。

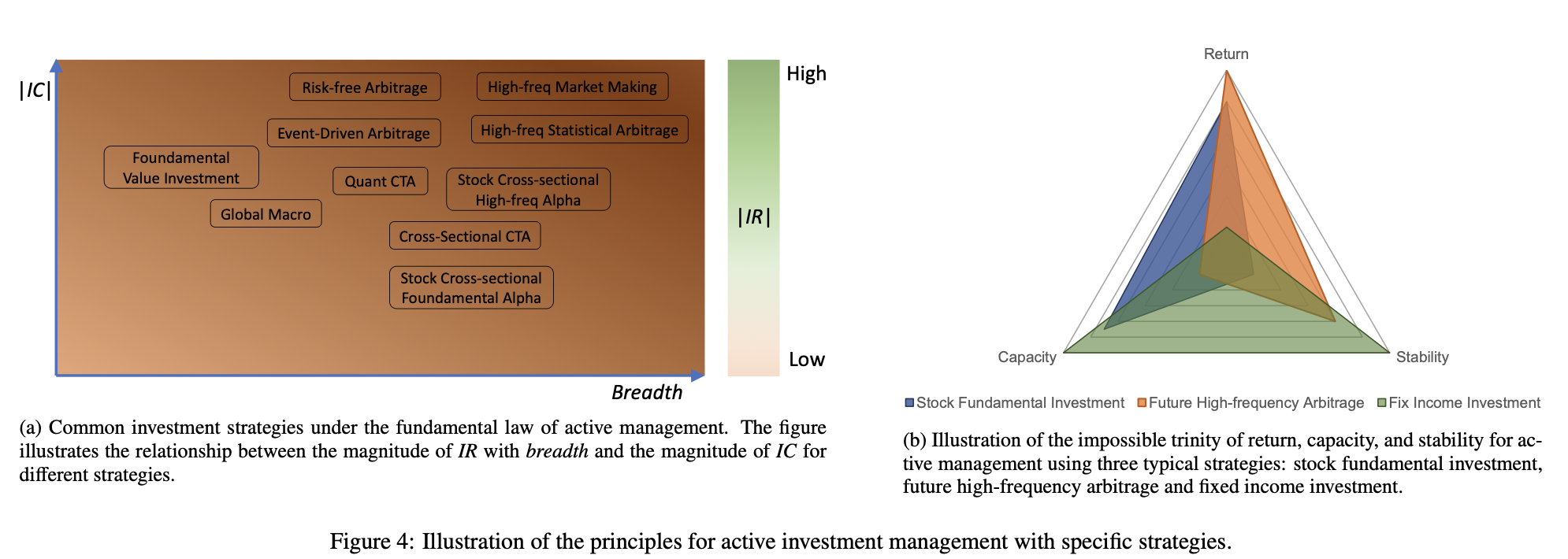
上图显示了各种策略在信息系数（IC）和广度上的分布情况，以及它们相应的信息比率（IR）绩效。横轴表示IC，纵轴表示广度，不同颜色和形状的点代表不同的策略。可以看出，一些策略在IC上表现优秀，但广度较小，而另一些策略则在广度上表现出色，但IC相对较低。图中的虚线轨迹表示了不同IR值的等高线，这表明了在IC和广度的空间中，IR的取值范围。从这个图中可以看出，最优的策略通常在IC和广度之间找到一个平衡，使IR达到最大值。

投资的不可能三角

第二个原则是资产管理的不可能三角。具体而言，任何投资策略都不能同时满足以下三个条件，即高回报、低风险（或等效地高稳定性）和高容量。图4b使用一个雷达图展示了不可能三角，其中包括三个变量：回报、稳定性和容量。例如，高频市场做市和日历套利策略可能能够达到高回报和稳定性（低投资组合波动性），但其资产管理规模的容量通常很小，即使在全球交易中，其资产规模通常也难以超过数十亿美元。相反，股票基本面策略的容量高，可达数万亿美元，但其回报和稳定性不如高频交易。上图通过一个雷达图展示了投资的不可能三角，其中包括三个关键变量：回报、稳定性和容量。不同颜色的区域代表不同的投资策略。可以清晰地看到，任何一种策略都无法同时在这三个方面取得最优的表现。投资者需要在这三者之间找到一个平衡，根据自己的风险偏好和目标来选择合适的策略。

量化投资的历史

量化投资的起源可以追溯到一个多世纪前，当时法国数学家路易斯·巴舍利耶于1900年发表了他的博士论文《投机理论》[17]，展示了如何使用概率法则和数学工具来研究股票价格的变动。作为首位探索将高等数学应用于金融市场的先驱，巴舍利耶的工作激发了量化金融学术研究的兴起，尽管由于当时数据稀缺而未在实际行业中得到广泛应用。量化投资首次由美国数学教授爱德华·索普（Edward Thorp）实践，他运用概率理论和统计分析赢得了二十一点游戏，并随后将他的研究应用于寻求股市中系统性和稳定的回报[18]。在这一小节中，我们通过两个方面介绍量化金融发展的历史和里程碑：学术界的研究里程碑和实际行业实践中量化投资的演变。

Q-Quant 和 P-Quant

学术界和投资业将量化金融分为两个分支，通常被称为“Q-Quant”和“P-Quant”。这两个分支分别基于风险中性度量和概率度量进行建模，因此得名。一般来说，Q-Quant研究的是衍生品定价问题，并对当前情况进行外推，采用以模型为驱动的研究框架，数据通常用于调整模型的参数。另一方面，P-Quant研究的是量化风险和投资组合管理，对未来进行建模，采用以数据为驱动的研究框架，构建不同的模型以改进对历史数据的拟合。通常情况下，Q-Quant研究在卖方机构（如投资银行和证券公司）进行，而P-Quant则在买方机构（如共同基金和对冲基金）中较为流行。表1比较了这两种类型的量化的特点。

表1：P-Quant和Q-Quant的比较 [19]

类型	目标	场景	度量	建模	例子	算法	挑战	业务
Q-Quant	外推当前	衍生品定价	风险中性度量	连续随机过程	Black-Scholes模型	Ito微积分，PDE	校准	卖方
P-Quant	模拟未来	投资组合管理	概率度量	离散时间序列	多因子模型	统计，机器学习	估计/预测	买方

Q-Quant的里程碑

1965年，美国经济学家、1970年诺贝尔经济学奖得主保罗·萨缪尔森（Paul Samuelson）引入了随机过程和随机微积分工具来分析金融市场和建模股票价格的随机变动[20]，并在同年发表了一篇研究生命周期投资组合选择问题的论文，采用了随机规划方法[21]。在同一年，另一位美国经济学家罗伯特·默顿（Robert Merton）也发表了他的生命周期投资组合选择工作。与萨缪尔森使用离散时间随机过程的方法不同，默顿的工作使用了连续时间随机微积分来对投资组合的随机不确定性进行建模[22]。几乎在同一年，经济学家菲舍尔·布莱克（Fischer Black）和迈伦·肖尔斯（Myron Scholes）证明了通过动态调整投资组合可以消除资产管理的预期收益和风险，并因此发明了衍生品投资的风险中性策略[23]。他们将这一理论应用于实际市场交易，并于1973年发表。这一风险中性模型后来以他们的名字命名，并被称为Black-Scholes模型[24]，这是一个用于定价包含衍生品投资工具的金融市场的偏微分方程（PDE）工具。具体而言，Black–Scholes模型建立了一个控制欧式期权认购或欧式期权认沽价格演变的偏微分方程，如下：

$$ \frac{\partial V}{\partial t} + \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 $$

其中V是期权价格作为股票价格S和时间t的函数，r是无风险利率，σ是股票的波动率。这个偏微分方程有一个闭合解，被称为Black-Scholes公式。由于罗伯特·默顿是第一位发表一篇扩展期权定价模型数学理解的论文的人，他通常也被认为对这一理论的贡献功不可没。默顿和肖尔斯因为发现风险中性动态修订而获得了1997年的诺贝尔经济学奖。后来，原始的Black-Scholes模型进行了扩展，以适应确定性可变利率和波动率，并进一步用于表征支付股息的工具的欧洲期权价格，以及美式期权和二元期权。

作为风险中性理论的开创性工作，Black-Scholes模型有许多局限性之一是对衍生品期限内基础波动性恒定且不受基础证券价格水平变化的假设。这一假设通常与隐含波动率曲面的微笑曲线和偏斜形状现象相矛盾。放宽恒定波动性假设是一个可能的解决方案。通过使用随机过程表征基础价格的波动性，可以更准确地实践建模衍生品，这个想法导致了有关随机波动性的一系列作品，如Heston模型[25]和SABR模型[26]。作为一种常用的随机波动性模型，Heston模型假设波动性过程的变化与方差本身的平方根成正比，并表现出向方差的长期均值回归的趋势。另一种常用的随机波动性模型是SABR模型，在利率衍生品市场中广泛使用。该模型使用随机微分方程来描述单一远期（例如LIBOR远期利率、远期掉期利率或远期股票价格）及其波动性，并具有再现波动率微笑曲线效应的能力。近年来，深度学习和强化学习技术被应用于与风险中性Q-Quant建模相结合。汉斯·比勒（Hans Buehler）引入了学习交易的概念，提出了深度对冲模型[27]，这是一个在存在市场摩擦（如交易成本、市场影响、流动性限制或风险限制）的情况下对衍生品组合进行对冲的框架，并使用深度强化学习和市场模拟对波动性随机过程进行建模。它不再使用公式，而是自然地捕捉相关市场参数的共同变动。

除了衍生品定价模型外，市场效率理论和风险建模理论在Q-quant中同样非常重要，无论是在学术界还是行业中。在1980年代，哈里森（Harrison）和普利斯卡（Pliska）建立了资产定价基本定理[28]，为有效市场无套利和完备市场提供了一系列必要和充分的条件。2000年，李大卫（David X. Li）引入了统计模型高斯Copula [29] 来评估衍生品定价和投资组合优化的风险价值（VaR），特别是抵押债务证券（CDO）。高斯Copula迅速成为金融机构用于相关多个金融证券之间关系的工具，因为即使对于以前难以定价的复杂资产，如抵押贷款，它在建模上相对简单。

P-Quant的里程碑

Q-quant在量化金融中起着极其重要的作用。然而，在本文中，我们站在买方的角度，关注资产预测和投资组合优化问题，因此，除非另有说明，否则以下关于量化投资的所有讨论都是基于P-quant的观点。

P-quant的起源始于现代投资组合理论的建立，该理论由哈里·马科维茨引入。该理论最初在他的博士论文“投资组合选择”中提出，并于1952年在《金融杂志》上发表[31]，随后在1959年的著作《投资组合选择：投资的有效分散》[32]中得到扩展。根据古老的格言“不要把所有的鸡蛋放在一个篮子里”，马科维茨提出了金融市场资产投资的有效前沿概念，并通过将其数学化为一个二次优化问题来最大化投资组合在某一水平上的预期收益（通常由投资组合中资产的方差来衡量）。

基于现代投资组合理论，资本资产定价模型（CAPM）随后由杰克·特雷诺（Jack Treynor，1961、1962年）[33]、威廉·夏普（William F. Sharpe，1964年）[34]、约翰·林特纳（John Lintner，1965年）[35]和简·莫辛（Jan Mossin，1966年）[36]独立提出。CAPM的目标是描述市场的系统风险与资产预期回报之间的关系。

$$E(R_p) - R_f = \alpha + \beta \cdot (E(R_m) - R_f)$$

其中\(E(R_p)\)是投资组合的预期回报，\(R_f\)是无风险回报，\(E(R_m)\)是市场的预期回报。具体而言，CAPM将资产回报和风险分解为两个独立的部分，即alpha和beta。Alpha衡量投资组合相对于基准指数（例如S&P500指数）的表现，而beta衡量投资组合相对于基准指数的方差，表征市场波动引起的风险。CAPM的主要贡献者之一，威廉·夏普与哈里·马科维茨一同获得了1990年的诺贝尔奖。量化金融的另一个重要步骤是麻省理工学院经济学家斯蒂芬·罗斯于1976年提出的套利定价理论（APT）。APT通过进一步引入多因子模型框架，以建立资产价格与各种宏观经济风险变量之间的关系，改进了其前身CAPM。在多因子模型框架下，诺贝尔奖得主尤金·法马在1992年与芝加哥大学同事肯尼斯·弗伦奇共同提出了著名的Fama-French三因子模型。

$$E(R_p) - R_f = \beta_0 + \beta_1 \cdot (E(R_m) - R_f) + \beta_2 \cdot SMB + \beta_3 \cdot HML$$

该模型建立了预期投资组合回报（减去无风险回报的期望值）与三个系统风险因素的关系：预期市场回报 \(E(R_m) - R_f\)，规模 \(SMB\)（小市值股票与大市值股票之间的差异），账面市值比 \(HML\)（高账面市值公司与低账面市值公司之间的差异）。三因子模型随后于2015年扩展为法马和弗伦奇五因子模型，添加了两个因子：盈利能力（最盈利公司与最不盈利公司之间的回报差异）和投资冒险性（保守性投资公司与激进性投资公司之间的回报差异）。

与多因子模型的进展平行，1980年代出现了许多关于时间序列分析的重要研究。1980年，诺贝尔奖得主克里斯托弗·辛姆斯引入了向量自回归（VAR）模型到经济学和金融领域。作为时间序列分析中常用的单序列自回归（AR）模型和自回归滑动平均（ARMA）模型的扩展，VAR特征化了随时间在多个时间序列之间的自回归属性，并假定回归公式中误差项的方差恒定。1982年，罗伯特·恩格勒引入了自回归条件异方差（ARCH）模型，并将其扩展为广义自回归条件异方差（GARCH）模型，通过在模型中指定随机方差来特征化市场中的金融波动模式。1987年，他与克莱夫·格兰杰（Granger因果关系发现者，用于建模多个时间序列之间的先导滞后模式）共同引入协整法进行测试金融时间序列中均值回归模式的显著性，协整检验已广泛用于发现统计套利策略的有希望的资产对。恩格勒和格兰杰因其在时间序列分析方面的贡献于2003年共同获得了诺贝尔奖，该分析在量化金融中用于市场预测和投资研究。

在2018年，三位深度学习技术的先驱者，Yoshua Bengio、Geoffrey Hinton和Yann LeCun获得了图灵奖。如今，深度学习已被学术研究人员广泛应用于金融领域，金融机构的量化研究人员使用深度学习构建复杂的非线性模型，以学习金融信号与预期回报之间的关系，并预测资产价格，其在拟合大数据方面的强大能力显著提高了市场预测和投资组合管理的性能。

尽管准确预测资产价格未来趋势是P-Quant中非常重要的任务，但量化研究人员更关注如何解释模型预测的效果以及解释模型真正起作用的方式，因为在投资组合经理的风险管理中，“why”比“what”更为关键。因果效应分析[39]和因子重要性分析是量化模型解释中的两个核心任务。克莱夫·格兰杰于1969年发明了格兰杰因果关系测试[40]，用于确定一个时间序列是否对预测另一个时间序列有用。尽管有关格兰杰因果关系测试是否能够在统计学上评估“真实”的因果关系存在争议，但该方法已被广泛应用于量化研究，例如搜索和评估具有显著先导滞后效应的股票对，并通过相应的策略进行交易。在1994年，Guido Imbens和Joshua Angrist引入了局部平均处理效应（LATE）模型，以表征经济学、金融学和社会科学中的统计因果效应，他们于2021年共同获得了诺贝尔经济学奖。因果推断领域的另一位重要贡献者是图灵奖得主裘德亚·珀尔，他发明了因果图（贝叶斯网络），可用于挖掘多因子模型中因素和回报之间的因果关系。另一方面，在因子重要性分析领域，Shapley值已成为衡量复杂非线性机器学习模型中单个特征贡献的重要标准。实际上，这个标准最初是由劳埃德·沙普利提出的，他是博弈论研究的诺贝尔奖获得者，也是合作博弈过程中个体玩家/代理的贡献度的衡量标准。

量化投资产业的昨天、今天与明天

发展历程

量化投资基金的蓬勃发展始于1990年代，伴随着互联网的兴起和交易所电子交易的发展。在这里，我们简要介绍了量化运作模型的演变，并将其分类为三代，分别标记为Quant 1.0–3.0，并总结它们的特点如图7所示。

• Quant 1.0出现在量化投资的早期阶段，但在当前市场仍然是最流行的量化运行模式。Quant 1.0的特点包括：

  1. 小而精干的团队，通常由经验丰富的投资组合经理领导，由一些具有强大数学、物理或计算机科学背景的研究员和交易员组成；
  2. 运用甚至发明数学和统计工具来分析金融市场，发现定价错误的资产进行交易；
  3. 交易信号和交易策略通常简单、可理解且可解释，以减少建模中的样本内过拟合风险。这个运作模型在量化交易上效率高，但在管理上鲁棒性低。特别是，Quant 1.0团队的成功过于依赖特定的核心研究员或交易员，这样的团队可能会随着天才的离开而迅速衰退甚至破产。此外，这样一个小的“策略研究室”限制了对复杂投资策略的研究效率，如依赖于多样化的金融数据类型、极大数据量和超大规模深度学习模型等复杂建模技术的量化股票alpha策略。

• Quant 2.0将量化运作模型从小规模的研究室变为产业化和标准化的alpha工厂。在这个模型中，数百甚至数千名投资研究员共同致力于从众多金融数据中挖掘有效的alpha因子[41]，使用标准化的评估标准、标准化的回测过程和标准化的参数配置。这些alpha挖掘研究员通过提交符合标准的alpha因子而获得奖励，这些alpha因子通常具有较高的回测收益、较高的夏普比率、合理的周转率和与alpha数据库中现有因子的低相关性。传统上，每个alpha因子都是一个数学表达式，表征某些股票的模式或特征，或者股票之间的某种关系，尽管越来越多复杂的机器学习因子也在被挖掘。典型的alpha因子包括动量因子、均值回归因子、事件驱动因子、成交量-价格离散因子、增长因子等。许多由alpha研究员提交的alpha因子被投资组合经理合并到统计模型或机器学习模型中，通过适当的风险中性化找到最优资产仓位，期望在市场中获得稳定且有前途的超额回报。然而，大规模的团队工作会导致巨大的人力资源成本，并且随着团队规模的不断扩大，情况变得越来越严重。具体而言，我们可以预期发现的有效alpha因子的数量与团队规模大致呈线性趋势（实际上，在实践中，当积累的因子规模已经很大时，发现新的有效alpha因子变得越来越困难），但投资组合回报增长显著低于alpha数量和团队规模的扩大，导致利润率变得越来越小。这种现象由许多原因引起，如策略市场容量的限制、发现新的有效alpha因子的难度不断增加，甚至人类智能在策略空间中搜索所有可能性时的限制。

• Quant 3.0随着深度学习技术的迅速发展而出现，该技术在计算机视觉和自然语言处理等许多领域取得了成功。与Quant 2.0不同，后者将更多的研究工作和人力投入于挖掘复杂的alpha因子，Quant 3.0更加注重深度学习建模。通过相对简单的因子，深度学习仍然有潜力学习一个表现与Quant 2.0模型一样出色的预测模型，利用其强大的端到端学习能力和灵活的模型拟合能力。在Quant 3.0中，挖掘alpha的人力成本至少部分替代为计算力的成本，特别是昂贵的GPU服务器。但总体而言，这是一种更为长期高效的量化研究方式。

一文了解AI、机器学习、深度学习 大数据时代漫游指南

量化4.0

尽管量化3.0在一些策略场景，如高频股票和期货交易中取得了成功，但它有三个主要局限性。

1. 传统上，构建一个“好”的深度神经网络是耗时且劳动密集的，因为需要进行网络架构设计和模型超参数调整的大量工作，以及在交易端进行模型部署和维护的繁琐工作。
2. 从深度学习黑盒编码的模型中获取可理解的信息是一项挑战，这使其对那些关心金融市场机制并希望了解利润和损失来源的投资者和研究人员非常不友好。
3. 深度学习依赖极大量的数据才能表现出良好的性能，因此只有高频交易（或至少是具有大广度的中等横截面alpha交易）属于深度学习适应的策略池。这一现象阻碍了深度学习技术在低频投资场景（如价值投资、基本CTA和全球宏观）中的应用。

需要新的研究和新的技术来解决这些局限性，这促使了我们在本文中提出量化4.0的建议。我们相信，随着人工智能（AI）技术前沿的迅速发展，量化3.0的局限性很可能在未来得到解决，或者至少部分解决。量化4.0，作为下一代量化技术，正在实践“端到端全流程AI”和“AI创造AI”的理念，整合最先进的自动化AI、可解释AI和知识驱动AI，为量化行业描绘新的图景。

• 自动化AI旨在构建量化研究和交易的全流程自动化，以显著降低量化研究的劳动力和时间成本，包括数据预处理、特征工程、模型构建和模型部署，并显著提高研发的效率和可持续性。特别是，我们引入最先进的AutoML技术，自动化整个策略开发流程中的每个模块。通过这种方式，我们提出将传统的手工建模转变为 “算法生成算法，模型构建模型” 的自动建模工作流，并最终朝着“AI创造AI”的技术理念发展。除了AI自动化，另一个重要任务是使AI更加透明，这对于投资风险管理至关重要。

• 可解释AI，通常在机器学习领域简称为XAI，试图打开包围深度学习模型的黑匣子。纯粹的黑匣子建模对于量化研究是不安全的，因为人们无法准确评估风险。在黑匣子建模下，很难知道收益来自何处，是否依赖于某些市场风格，以及特定回撤的原因是什么。越来越多XAI领域的新技术可以应用于量化，以增强机器学习建模的透明性，因此我们建议量化研究人员更加关注XAI。我们必须注意，提高模型可解释性是有成本的。图9展示了通用性、准确性和可解释性的不可能三角形，告诉我们我们必须牺牲三角形中至少一个顶点，以从其他两个中获得好处。例如，物理定律 \(E = mc^2\) 建立了能量、质量和光速之间的可解释和准确关系，但这个公式只能应用于物理学的特定领域，并且牺牲了通用性。想象一下，如果我们在模型中提供更多的先验知识或领域经验，这相当于在同时保护准确性和可解释性的性能的前提下降低通用性。

• 知识驱动AI与依赖大量数据样本的数据驱动AI有所不同，后者适用于具有大广度的投资策略，如高频交易或股票横截面交易。它是对数据驱动AI技术（如深度学习，如图10所示，使用贝叶斯定理）的重要补充。在本文中，我们引入知识图，它以实体和关系组成的网络结构表示知识，并使用语义三元组存储知识。金融行为和事件的知识图可以通过符号推理和神经推理技术进行分析和推断，用于投资决策。这意味着在低交易频率但在信息收集和分析方面非常密集的投资场景，包括价值投资和全球宏观投资，具有潜在的应用前景。