Quant4.0(二)自动化AI与量化投研
量化4.0中的自动化AI涵盖了全量化流程的自动化。本节中我们首先介绍研发流程的全景,然后讨论如何将其升级到自动化AI版本。
本文是对论文Quant 4.0: Engineering Quantitative Investment with Automated, Explainable and Knowledge-driven Artificial Intelligence的部分翻译,有删改。原文地址
自动化投研流程
传统流程
数十年的发展使得量化研究形成了一个标准的工作流程,如图11所示(蓝色部分)。这个工作流程包括许多模块,包括数据预处理、因子挖掘、建模、组合优化、订单执行和风险分析。
数据预处理通常是量化研究中的第一步。原始数据可能存在许多问题。首先,金融数据通常有一些缺失记录。例如,在技术分析中,由于通信过程中的数据包丢失,您可能在某些时间点没有收到价格数据,或者由于股票停牌而在某些交易日错过了价格数据。同样,在基本分析中,由于未及时报告,您可能会错过部分财务报表数据。虽然可以使用传统的统计数据插补方法来估算和填补缺失的记录,但在插补过程中必须避免使用未来信息。其次,金融数据包含可能来自错误记录、数据存储问题、数据传输问题或极端市场的极端值和异常值,这些异常值可能导致投资决策中的风险偏差。异常值可以通过数据winsorization方法[43]进行消除,该方法限制在某个百分位范围内的极端值,但必须注意一些异常值实际上是量化交易的强烈信号而不是噪音,在数据预处理过程中必须区分这两者。第三,许多金融数据,如新闻事件数据,数据覆盖率低,更新频率不规律。我们必须将这些类型的数据与高覆盖率和常规频率的数据(如行情数据)对齐,以便于下游的因子挖掘和建模任务。第四,不同的数据特征在值范围上有很大差异,因此一些“大”特征可能在建模中占主导地位。因此,使用数据标准化方法来归一化特征的范围。在标准化数据的方式上必须注意以减少信息损失。
文章主要针对深度学习模型而写,事实上,梯度提升树模型就并不需要这些数据预处理。
因子挖掘是特征工程的一项任务[44],它利用金融和经济领域的知识,从原始数据中设计、搜索或提取因子(用于下游建模的特征)。通常,较大的因子值表示更显著的交易信号。因子挖掘的动机是从原始数据中找到这些信号,用于市场预测,并提高下游建模任务的质量。传统上,金融因子可以表示为代数公式或基于规则的表达式。让我们以一个简单的股票alpha因子为例。
$$ \text{factor} = -\text{ts\_corr}(\text{rank}(\text{close}), \text{rank}(\text{volume}), 50) $$
其中ts_corr()函数使用前50个交易日的数据计算每日收盘价和成交量的相关性,表示收盘时间序列和成交量时间序列的趋势有多相似。rank()函数将横截面中的值映射到它们的顺序,并根据它们的降序将它们归一化到 [−1, +1] 的范围内,以消除极端值的影响。该因子倾向于在它们的价格和成交量方向相反时选择那些股票,其背后的思想是基于这样一个假设:没有成交量增长的支持,价格趋势无法持续。传统上,因子挖掘是一项劳动密集型的工作。大多数量化研究人员一年内只能发现有限数量的“好”因子。不同的金融机构对于“好”因子有不同的定义或标准,但它们大多考虑一些共同的方面,如收益、夏普比率、最大回撤、换手率和与其他因子的相关性[41],此外,一些机构要求这些因子在经济学上必须有意义、可理解和可解释。
建模是利用因子构建统计或机器学习模型,用于预测市场趋势、资产价格变动、最佳交易时机或最有/最无价值的资产。通常,通过回测实验评估预测模型,该实验使用历史数据模拟预测和交易过程。在选择模型时,必须考虑多个因素,如预测准确性、模型可解释性、模型稳健性和计算复杂性,并根据最终目标找到最佳权衡。特别是,我们必须注意,大多数统计或机器学习模型并非专门为金融时间序列开发,因此我们必须调整这些模型在量化建模中的应用。首先,金融时间序列的预测必须避免使用未来信息,因此我们更倾向于前向验证[45](将时间序列划分为训练、验证和测试块)而不是模型超参数优化中的交叉验证。其次,金融时间序列通常显著非平稳,远离许多机器学习模型所需的独立同分布(i.i.d.)假设。因此,需要进行数据转换,使数据分布更接近i.i.d.,如果可能的话,更像正态分布。第三,市场风格随时间变化,导致金融时间序列分布发生变化。因此,周期性地重新训练模型是必要的,以保持模型适应市场风格的变化。
投资组合优化的目标是找到最优的资产配置,以期同时获得高回报和低风险。虽然预测模型告诉我们何时买入/卖出或买入/卖出什么,但投资组合优化则指定了要买入/卖出多少。典型的投资组合优化器试图解决一个受限的凸二次规划问题,这是从马科维茨的有效边界理论推导出来的。
$$ \begin{array}{cl} \max _{w_{t}} & w_{t}^{T} r_{t} \\ \text { subject to } & w_{t}^{T} \Sigma w_{t} \leq C_{1} \\ & \left|w_{t}-w_{t-1}\right| \leq C_{2} \\ & 0 \leq w_{i, t} \leq C_{3} \leq 1, \text { for } i=1,2, \ldots, n \end{array} $$
其中\(r_t=(r_{1,t},r_{2,t},…,r_{n,t})^T\) 是时间\(t\)时各资产(例如股票)的收益,\(wt=(w_{1,t}, w_{2,t},…,w_{n,t})^T\) 是相应的仓位权重(资本分配的百分比)。\(C_1, C_2, C_3\) 是正约束边界。\(\Sigma\) 是时间\(t\)时\(n\)个资产收益的波动率矩阵。目标函数试图最大化投资组合回报并控制风险和换手率的上限(以减少交易成本)。这个优化问题的关键在于如何估计波动率矩阵\(\Sigma\),如果历史数据不够长,其估计通常是不稳定的,在这种情况下,降维技巧如正则化和因子化可以帮助提高估计的稳健性。
订单执行是以最优价格和最小市场冲击买入或卖出订单的任务。通常,一次性购买(或出售)大订单会推动目标资产价格朝着有害的方向变动(由这个大订单造成的市场冲击),因此增加了交易成本。一个广泛使用的解决方案是订单拆分,将大订单分成多个小订单,以减少市场冲击。算法交易为订单拆分提供了一系列数学工具,从最简单的时间加权平均价格(TWAP)和成交量加权平均价格(VWAP)到复杂的多智能体强化学习方法,其中最优的订单流被建模为(部分可观察的)马尔可夫决策过程。
风险分析是量化研究和量化交易中不可或缺的任务。我们必须发现并了解每种可能的风险暴露,以更好地控制量化研究和交易中不必要和有害的风险[47]。在监控模块中,风险是实时测量的,这些信息和分析被发送回来以帮助量化研究人员改进他们的策略。股票交易中最流行的风险模型是BARRA模型[48],它将投资组合波动性分解为许多预定义的风险因子的敞口,包括风格因子(大小、成长、流动性等)和行业因子。然而,BARRA模型只能解释总波动性的约30%,剩下的70%部分中隐藏着未知的风险。
自动化AI流程
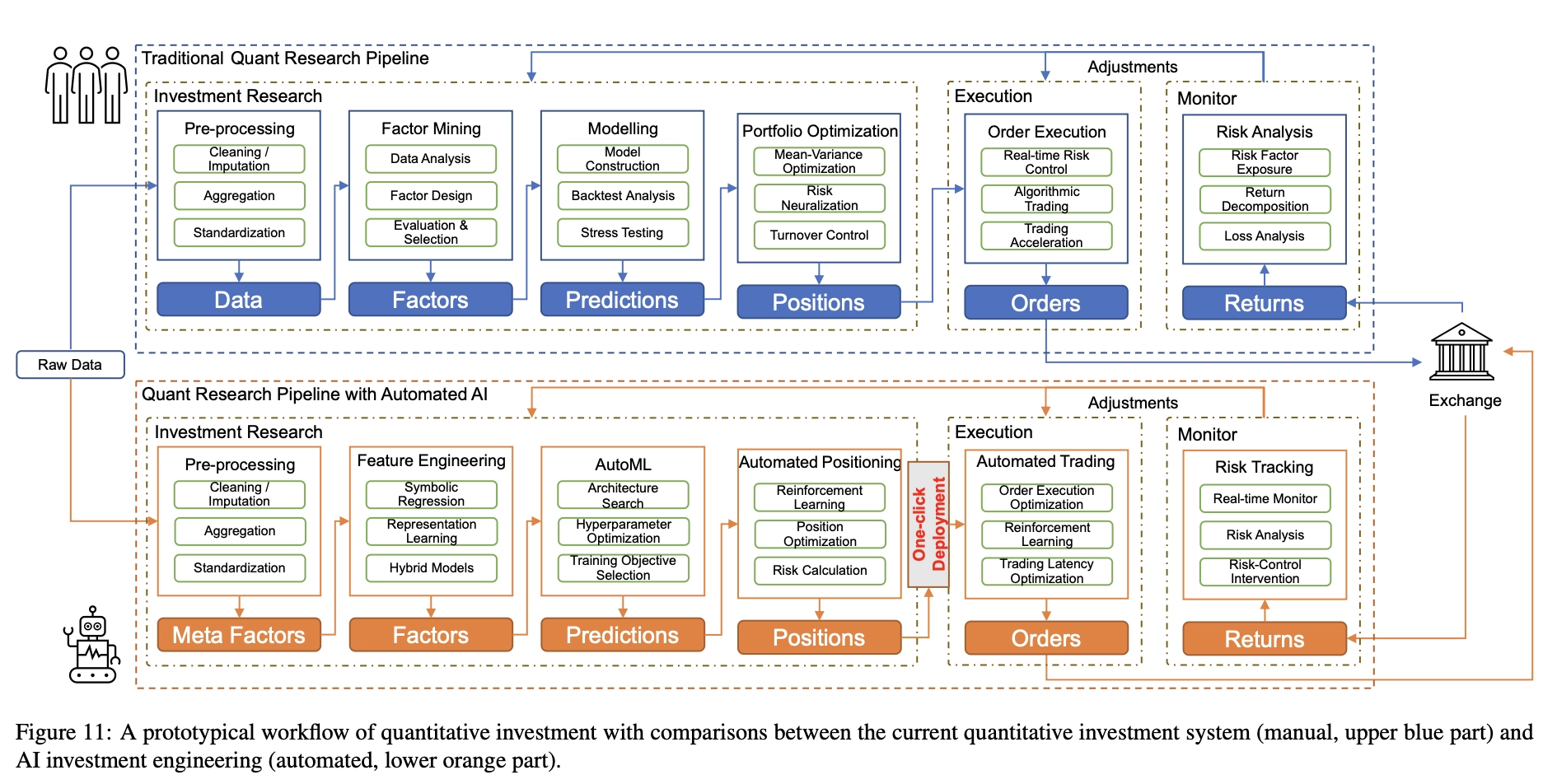
Quant 4.0的自动化流程如图11所示(橙色部分),其中流程中的模块通过应用最先进的人工智能技术实现自动化。在本节的后续部分,我们将集中讨论自动化流程中的三个核心模块。
- 自动因子挖掘:应用自动化特征工程技术搜索和评估从元因子生成的重要财务因子。我们将介绍流行的搜索算法,并演示如何设计算法工作流程。
- 自动建模:应用AutoML技术来发现最优的深度学习模型,自动选择最合适的模型和最佳的模型结构,并调整最佳的超参数。
- 一键部署:构建一个自动化工作流程,在计算资源有限的交易服务器上部署已训练的大型模型。它自动执行模型压缩、任务调度和模型并行化,为繁琐的“脏活”节省了大量的人力和时间。
自动化因子挖掘
对于量化领域的特征工程,指的是从原始数据中提取金融因子的过程,由于其固有的噪声特性,这些数据很难进行有效的模式识别[49, 50, 51]。传统上,具有显著“alpha”的金融因子是由量化研究人员手动探索和开发的,他们依赖专业领域知识和对金融市场的全面了解。尽管一些金融机构开始使用随机搜索或通用编程算法,但这些技术主要被用作小规模辅助工具,以帮助提高量化研究人员的工作效率。在Quant 4.0中,我们提出将因子挖掘过程自动化,将特征工程制定为一个搜索问题,并利用相应的算法在规模上生成具有令人满意的回测性能的因子。根据它们的表达形式,我们将因子分类为
- 符号[52] 因子,这些是符号方程或符号规则
- 机器学习因子,这些由神经网络表示,我们将在后续部分详细阐述。
符号因子
符号因子挖掘可以被视为符号回归[56]的一种特殊情况。传统的符号回归算法通常从给定的操作数和运算符中生成大量符号表达式,并选择最大化预定义目标函数的符号表达式。图12展示了自动化符号因子挖掘的框架,包括四个核心部分:操作数空间、运算符空间、搜索算法和评估标准。
操作数空间:定义了哪些元因子可以用于因子挖掘。元因子是构建因子的基本组成部分,典型的元因子包括基本价格和成交量信息、行业分类、从限价/委托簿中提取的基本特征、常见技术指标、来自财务分析师的基本统计数据、来自公开公司的公告、财务报告和其他研究报告、投资者情绪的情感信号[57, 58]等。
运算符空间:定义了在因子挖掘过程中可以使用哪些运算符。例如,在横截面股票选择中,运算符可以分为用于构建符号因子的主要运算符和用于在不同交易环境中对因子进行标准化的后处理运算符。主要运算符可以进一步分类为按元素运算符,例如 () 和 log(),时间序列运算符,例如 ts rank() 和 ts mean(),它们分别计算每支股票的秩次和均值,横截面运算符,例如 rank() 和 quantile(),它们计算在特定交易时间沿横截面的秩次和分位数,以及组运算符,例如 group rank(),它们分别计算每个组(例如行业或部门)中的秩次。后处理运算符用于“微调”生成的因子。典型的后处理运算符包括用于剪辑离群值的 winsorization [43] 和用于统一数据范围的标准化运算符,用于风险平衡的中性化运算符,用于限制股票选择范围的分组运算符,以及用于控制换手率从而减少交易成本的衰减运算符。
搜索算法:搜索算法旨在以尽可能高效的方式搜索和找到有效或合格的因子。生成新因子的一种简单方法是蒙特卡洛(MC)算法,该算法随机选择操作数和运算符空间中的元素,并递归生成符号表达式树。不幸的是,随着生成的公式的长度和复杂性的增加,搜索时间可能呈指数级增长,迫使我们考虑更有效的替代方案。第一选择是马尔可夫链蒙特卡洛(MCMC)算法 [59],该算法以重要性采样的方式从后验分布中生成因子,因此比MC更高效。第二选择是遗传编程 [61],这是一种用于采样和优化树状数据的特殊进化算法。第三个选择涉及基于梯度的方法,例如神经网络,它用连续非线性函数逼近离散的符号公式,并沿着梯度方向搜索,显著比随机搜索更高效。
评估标准:评估标准用于衡量搜索算法找到的因子的质量。通过回测实验评估生成因子的性能。典型的评估标准包括信息系数(IC)、基于信息系数的信息比率(ICIR),以及年化回报、最大回撤、夏普比率和换手率。此外,通过过滤与其他因子高度相关的冗余因子,保持因子之间的信息多样性是非常重要的。
机器学习因子
符号因子在实践中因其简单性和可理解性而被广泛使用。然而,它们的表示能力受到操作数和运算符的丰富性的限制。另一方面,机器学习因子在表示上更具灵活性,以适应更复杂的非线性关系 [67],因此它们有机会在市场预测中表现更好。特别是,挖掘机器学习因子 [68, 69, 70, 71] 是一个拟合神经网络的过程,其中梯度提供了快速搜索解决方案的最佳方向。如图 15 所示,大多数用于股票预测的深度神经网络都遵循编码器-解码器架构 [72],其中编码器将元因子映射到潜在矢量表示,解码器将此嵌入转换为某些结果,如未来回报 [73]。事实上,不仅最终结果,嵌入本身也可以用作(高维)机器学习因子 [74],并进一步应用于各种下游任务。
机器学习因子也有一些局限性。首先,由于机器学习的黑盒性质,它们通常难以解释和理解。其次,神经网络使用的梯度搜索可能会陷入某些局部最优并导致模型不稳定性问题。最后,由于其灵活性,神经网络可能更容易受到过拟合的影响,而在量化领域,由于数据极其嘈杂,情况变得更加严重。
无论是自动挖掘符号因子,还是直接拟合机器学习因子,都是纯粹由数据驱动的方法。而这在极低信噪比金融数据上想要获得成功,需要人工引入大量先验知识。
自动化建模
统计机器学习的自动化,如支持向量机(SVM)、决策树和提升,已经得到了广泛研究。一种简单而直接的自动化方法是对所有可能的配置进行枚举,其中包括机器学习算法的选择和相应的超参数。在本文中,我们专注于最先进的深度学习自动化问题,这由于建模中的端到端性质和网络架构问题而更加复杂。深度学习模型的配置包括三个部分:架构、超参数和目标,它们共同决定了模型的最终性能。传统上,这些配置是手动调整的。在Quant 4.0中,它们通过各种AutoML算法进行搜索和优化。标准的AutoML系统需要回答以下三个问题:要搜索什么(即,搜索空间)、如何搜索(即,搜索算法)、为什么要搜索(即,性能评估)。
搜索空间
搜索空间是为需要以自动方式优化的三个配置设置而设计的。
架构 配置了网络结构。例如,多层感知器的架构由隐藏层的数量和每个层的神经元数量指定。卷积神经网络的架构需要考虑更多的配置,如卷积核的数量以及它们的步幅和接受域。大规模模型(如Transformer)的架构由许多预定义的块(例如自注意力块、残差块)组成。正如上文所述,架构是复杂的,可能在不同尺度上具有分层结构。因此,搜索空间可以在不同的粒度上定义,从卷积和注意力等低级运算符到LSTM单元等高级模块。早期的搜索算法在最细的粒度上运行,并优化神经网络的低级结构。这样的搜索过程在网络结构上灵活,但在整合先验知识和抽象方面效率较低。一种解决方案是在网络架构中假设分层结构。具体而言,在高层次上,网络被设计成细胞的图(即块/主题 [42, 80]),每个细胞都是一个子网络。为了降低计算成本,许多细胞在低层次上共享相同的内部结构。基于细胞的搜索算法 [81, 82] 需要找到细胞之间的高级结构以及细胞内的低级结构。
超参数 控制整个训练过程。例如,学习率确定了向损失函数最小值迈进的步长。较小的学习率在解中更精确,但收敛较慢。批量大小确定了用于梯度估计的批次中涉及的样本数量,这也影响训练的效率和稳定性。与架构的搜索空间相比,超参数的搜索空间更简单,因为大多数超参数是连续的(例如学习率)或近似连续值(例如批量大小)。
目标 指定了训练过程中使用的损失函数和标签。损失函数是机器学习模型的关键组件,因为它提供了模型应该训练到的目标。除了经典的损失函数,如均方损失和交叉熵损失外,还可以选择专为量化任务设计的新损失函数。标签定义了模型旨在拟合的“ground-truth”目标。例如,在搜索空间中可以考虑不同持有时间窗口内的价格涨跌或未来收益。
在资产定价领域选择/设计损失函数的难度超乎想象。传统机器学习算法的优化目标是模型对单样本预测误差最小化,而实践中则是要考察投资组合夏普比,预测误差的协方差与均值同样重要。不仅如此,与一般任务相比,量化选股的标签数量不仅少,而且大部分由噪声构成。简单地套用已有的损失函数,与样本内投资组合表现并无一致性,遑论样本外,在这一点上亟需金融理论的突破,自动化机器学习技术对此无能为力。
搜索算法
在给定搜索空间的情况下,我们可以使用搜索算法找到最佳的模型配置。表2列出了各种类型的搜索算法及其相应的任务:网络架构搜索(NAS)[75]、超参数优化(HPO)[83] 和训练目标选择(TOS)。网格搜索是一种蛮力算法,它在配置的网格上进行搜索并评估其中的所有配置。由于实现和并行化的简便性,当搜索空间较小时,它是一个不错的选择[84]。然而,深度学习中的大多数NAS和HPO问题都有极大的搜索空间,网格搜索无法很好地扩展到这些问题。此外,网格搜索在HPO和TOS中的使用较在NAS中更为普遍,因为除了列举所有可能性外,NAS的搜索空间很难进行网格布局。
随机搜索 使用一些随机采样机制(如蒙特卡洛或MCMC)生成若干候选配置。它非常直观易懂,并且易于实现和并行化(主要用于独立采样机制,如蒙特卡洛采样或重要性采样)。随机搜索非常灵活,可用于NAS、HPO 和 TOS。虽然随机搜索通常比网格搜索快[84],但在处理高维搜索空间时仍然很困难,因为潜在配置的数量随着超参数数量的增加呈指数增长。
进化算法 是随机搜索的一种扩展。它利用进化机制迭代地改进模型配置。它将网络架构编码为一个种群,并在其上执行进化步骤以迭代地改进模型。具体而言,模型首先根据其底层计算图进行编码。然后,一组预定义的进化操作被应用于编码的模型,包括结构修改,例如插入或删除多个操作和添加跳过连接,以及与超参数相关的操作,如学习率调整。在每次迭代中,通过锦标赛选择表现最佳的模型,并通过突变和交叉操作组合它们以形成下一代。进化算法固有地支持代际间的权重继承,有助于加速训练的收敛并提高搜索效率。
贝叶斯优化 通过利用替代模型来更有效地探索无法明确表达的目标函数的搜索空间。具体而言,对于HPO的黑盒目标函数,贝叶斯优化使用替代函数(如高斯过程或树状Parzen估计器)初始化先验分布。然后从先验分布中(带有重要性)采样新的数据点,并使用底层目标函数计算它们的值。给定这些新样本和先验,可以计算后验函数,并用作更新后的替代函数以替代原始先验函数。此过程重复进行,直到找到最优解。传统上,贝叶斯优化用于连续搜索任务,如HPO,但最近的研究也将其扩展到了NAS任务。
基于梯度的方法 在目标函数的梯度存在时非常高效。然而,对于NAS,搜索空间是离散的,不能直接定义梯度。一个解决方案是“软化”体系结构并定义一个超参数化的“超体系结构”,它涵盖所有可能的候选者并且是可微的。典型的基于梯度的NAS方法是DARTS [97],它构建了一个超参数化网络,其中计算图上包含所有类型的候选操作。结果值是所有操作结果的加权和,其中权重是参数化概率向量的softmax值。通过双层优化问题,训练模型参数和体系结构参数。在推理过程中,选择具有最高概率的体系结构和超参数。在NAS和HPO任务中,DARTS比随机搜索和强化学习快得多。
自动化的复杂模型设计固然令人兴奋,但在样本内预测性能提升的同时,更要考虑回测过拟合风险
加速评估
自动模型搜索的计算成本来自两个部分:搜索算法和模型评估,而后者通常是计算的瓶颈,因为在给定配置下训练深度神经网络直至收敛是非常耗时的。在先前的研究中引入了几种方法来解决这个问题。首先,神经网络的训练过程可以在收敛之前提前停止,以减少评估的计算时间[81]。其次,模型可以选择更少的样本来加速训练过程[94]。第三,可以使用热启动模型训练来利用已选择模型的信息[102],或者继承超参数化的“父”模型[103, 97, 98]的信息以加速搜索循环。
自动化部署
模型部署是将开发的模型从离线研究转移到在线交易的任务。这不仅仅涉及代码和数据的传输,还包括数据和因子依赖性的同步,适应交易服务器和系统,调试模型推断,测试计算延迟等等。在接下来的部分中,我们专注于模型部署中的一个重要问题:如何加速深度学习推断以适应高频交易和算法交易场景。我们提出了一种自动一键部署的解决方案,利用诸如模型编译[104]和模型压缩[105, 106]等技术来实现推断加速[104, 105, 106]。前者使推断更快,而不改变模型本身,后者则寻找更小、更轻的替代模型以节省推断时间。
模型编译加速
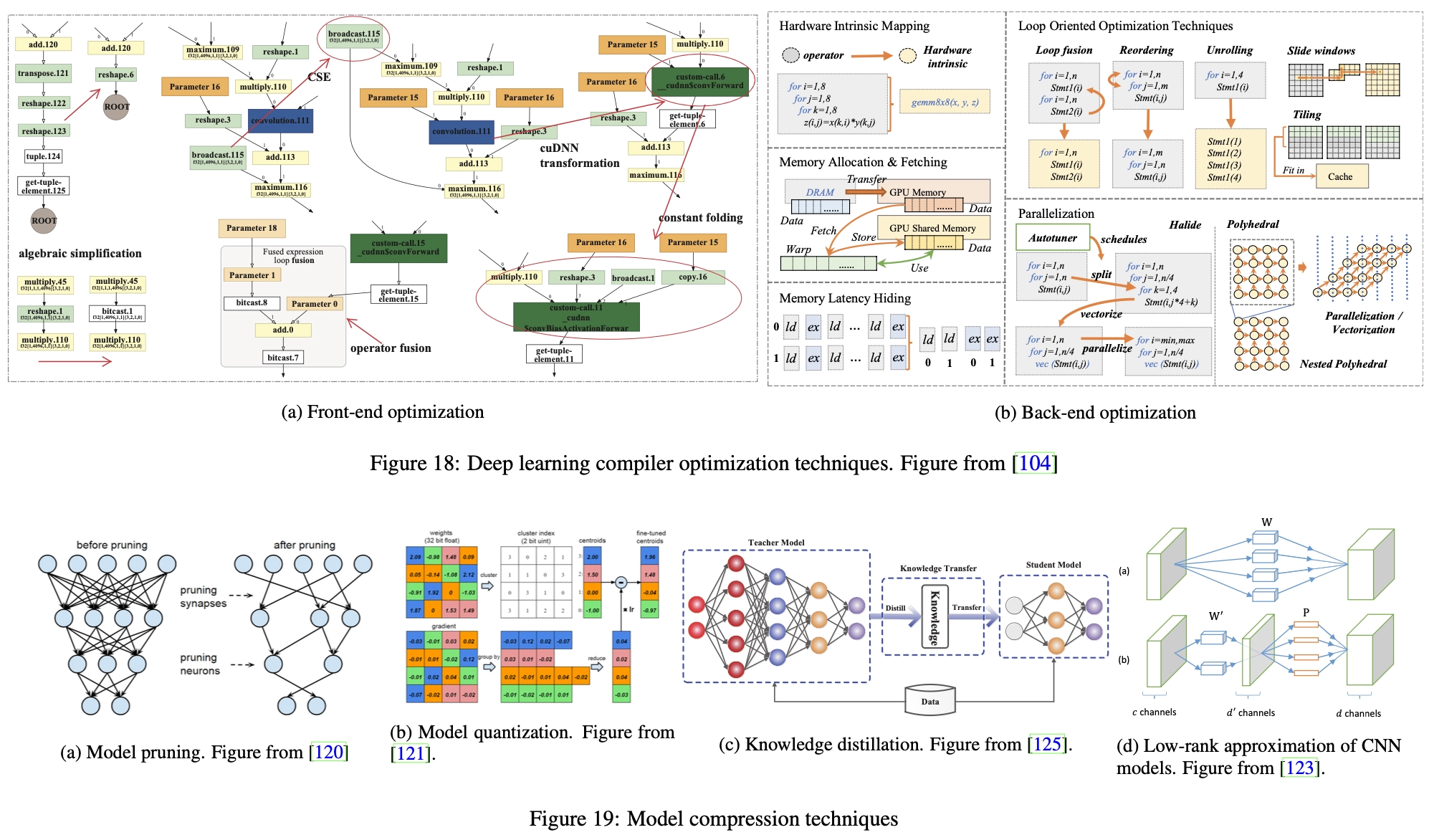
在开发阶段,深度学习模型的功能是实现计算的底层框架的首要任务。因此,在这个阶段,框架将所有操作严格映射到计算图中。然而,这种直接映射在计算固定的部署阶段引入了大量的优化空间。因此,模型的计算可以在不损害其原始语义的情况下得到极大简化,并适应硬件特性。这种优化是深度学习编译器[107, 108, 109]中的主要主题之一,可以分为前端优化和后端优化,它们分别在深度学习模型的高级和低级中间表示(IRs)上工作。根据[104]的总结,我们将简要介绍相关的优化技术。
前端优化,如图18a所示,侧重于简化计算图的结构。例如,代数简化技术,如常量折叠[110]和强度减少[111]通过变换或合并将昂贵的操作转换为廉价的操作。公共子表达式提取(CSE)[112]技术识别计算图中的重复节点,并将它们合并成一个节点,以避免重复计算。
后端优化,如图18b所示,侧重于硬件架构的特性,如局部性和内存延迟。例如,预取技术[113]从主内存加载数据到GPU,然后将它们需要之前的速度提高。基于循环的优化[114]在循环内部重新排列、融合和展开操作,以增强相邻指令之间的局部性。内存延迟隐藏[115]技术旨在提高指令吞吐量,以减轻访问内存时的高延迟问题。并行化技术,如循环分割[116]、自动矢量化[117]和循环偏斜[118, 119],也可以应用于最大程度地利用现代处理器提供的并行性。
模型压缩加速
模型压缩的目标是在减少性能下降的同时减小推断时的模型大小。这样,压缩后的模型可以被视为原始模型的近似。一般来说,模型压缩可以在微观和宏观两个层面上进行,前者关注单个模型参数的精度,后者关注简化整体模型结构。
在微观层面上,可以应用修剪和量化技术来减少参数的数量和单个参数的位数。模型修剪[120],如图19a所示,移除在神经网络中对神经元的激活影响不大的不重要的连接和神经元。候选参数的识别通常基于其权重,其中权重较小的参数被考虑进行修剪。模型量化[121],如图19b所示,将参数从浮点数转换为低位表示。具体而言,构造一个代码簿,根据所有参数值的分布存储原始参数的近似值。然后,根据代码簿对参数进行量化,从而减小参数的位数。由于精度降低引起的性能下降是不可避免的,压缩后的模型通常会经过重新训练,以接近其原始性能。
在宏观层面上,模型可以通过知识蒸馏[122]和低秩分解[123, 124]等技术显著压缩成一个较小的模型,具有更简单的体系结构。知识蒸馏(图19c)通过从原始大模型(称为教师模型)向一个小且简单的模型(称为学生模型)传递有用的知识来压缩模型,最小化知识丢失。低秩分解技术(图19d)假设模型参数的稀疏性,然后将原始神经网络的参数矩阵分解为低秩矩阵的点积,从而较少模型复杂度。
深度学习模型编译和压缩技术是部署深度学习模型的重要通用优化技术,但通常,量化交易并非高请求量的任务,模型推理也不是卡点和难点,为此投入精力做损失模型精度的性能优化可能得不偿失。
Quant4.0(二)自动化AI与量化投研