排序学习（LTR）简明：从RankNet到LambdaMART

本文简要介绍了排序学习的背景、分类、性能度量，并归纳其发展历程中的几种经典算法。本文不追求深入每个技术细节，而是注重传递排序学习核心概念的直观理解，为LTR不同场景下的实际应用做铺垫。

简介

背景

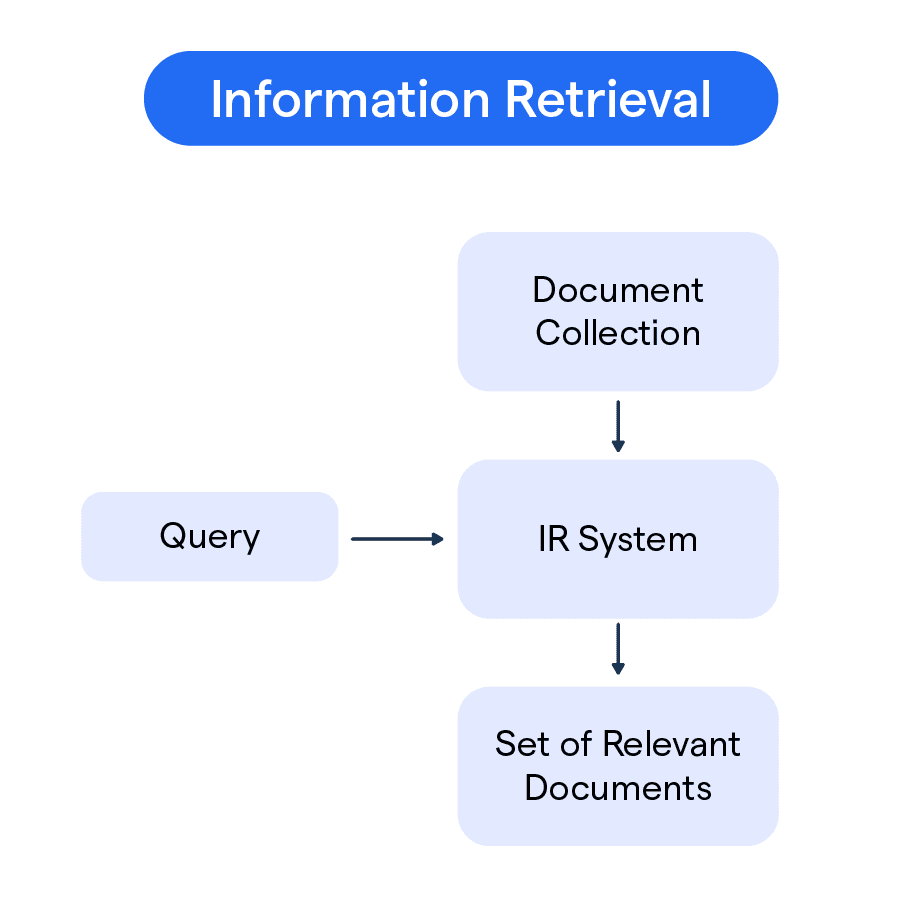
排序学习（Learning-to-Rank, LTR）是信息检索领域的关键技术。以搜索引擎为例，LTR用于提升最终结果质量，效果久经考验。每次检索时用户意图称为“Query”，候选结果称为“Document”，搜索引擎的目标是将最相关，最高质量的结果放在首位，第二好的结果放在次位，依此类推。对于用户Query，IR系统首先从数据库（数十亿网页）召回可能与用户Query相关的文档，由于性能限制这一过程通常是分层、多路并行完成的，最底层可能就是简单的关键词匹配，而越上层的模型越复杂，最终出口队列候选数量下降到几十到几百。候选集需要排序后最终展现给用户，在这个场景下的算法目标与回归/排序模型迥异：

1. 文档的绝对相关性估计没意义，已经无法改变，只须考虑相对顺序
2. 大多数预测结果没意义，极少用户会翻上十几页，只有头部结果重要

因此引入排序学习。

分类

排序学习的实现可以分为三类：Point-wise, Pair-wise 和 List-wise。

Point-wise LTR 直接根据单个文档特征预测其相关性，使用均方误差/交叉熵损失，不考虑与其他文档的相关性。它可以被认为是一种伪LTR，优点是实现方便，且效果易于评估。本文不做赘述。

Pair-wise LTR 以预测文档间两两偏序关系为目标——只要每一对文档关系预测正确，列表也会是正确的——问题变成了二分类，使用交叉熵损失。相比Point-wise，它放弃了对绝对值估计，更擅长排序任务，代表算法有RankNet。

List-wise LTR 将整个文档列表视为一个整体，直接优化一个整体的目标函数，如归一化折现累积增益 (NDCG) 。这可以说是LTR的最终形态，它既绕过了绝对值估计的困难，又避免了尾部结果对模型的过分影响，代表算法有LambdaMART、ListNet。

性能度量

归一化折扣累积增益 (NDCG) 是LTR（Learning to Rank）中最常用的度量之一，尤其是在信息检索和搜索引擎中优化排名质量的目标下。它评估了排名模型在考虑文档相关性得分的情况下对文档排序的效果。

1. 累积增益 (CG)：对于一个排名的文档列表，CG 是列表中每个位置文档的相关性得分之和：

$$ \text{CG@k} = \sum_{i=1}^{k} rel(i) $$

其中 \(rel(i)\)是位置 \(i\)处文档的相关性得分，而 \(K\)是排名位置。

2. 折扣累积增益 (DCG)：DCG 对相关性得分应用了一个折扣因子，以考虑到列表中较低排名的文档通常对用户满意度贡献较小的事实：

$$ \text{DCG@k} = \sum_{i=1}^{k} \frac{rel(i)}{\log_2(i+1)} $$

分母 \(\log_2(i+1)\)随着 \(i\)的增加而减小。

3. 理想 DCG (IDCG)：IDCG 是理想排名（即相关性倒序排列）的 DCG。它作为规范化因子：

$$ \text{IDCG@k} = \sum_{i=1}^{k} \frac{rel_{\text{ideal}}(i)}{\log_2(i+1)} $$

4. 归一化 DCG (NDCG)：NDCG 是 DCG 与 IDCG 的比率，将分数标准化在 0 和 1 之间，其中 1 表示完美的排名：

$$ \text{NDCG@k} = \frac{\text{DCG@k}}{\text{IDCG@k}} $$

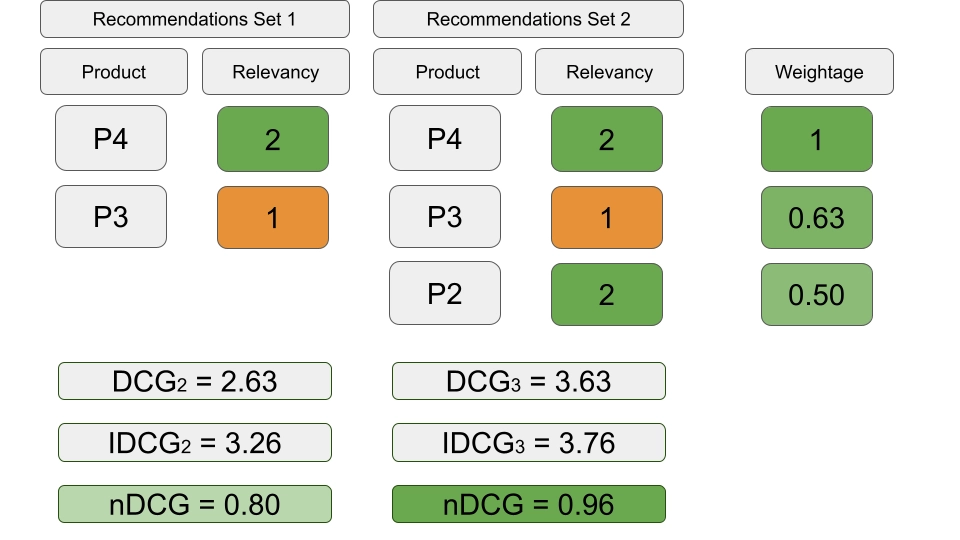
下图展示了计算NDCG的例子。

经典算法

RankNet

基础

Ranknet从结构上来看与一个普通进行二分类的多层神经网络没有任何区别，但是通过特殊的训练方式和优化目标，实现了对文档偏序关系的学习。RankNet的创新之处在于，用交叉熵损失建模本不适用梯度下降求解Ranking问题。

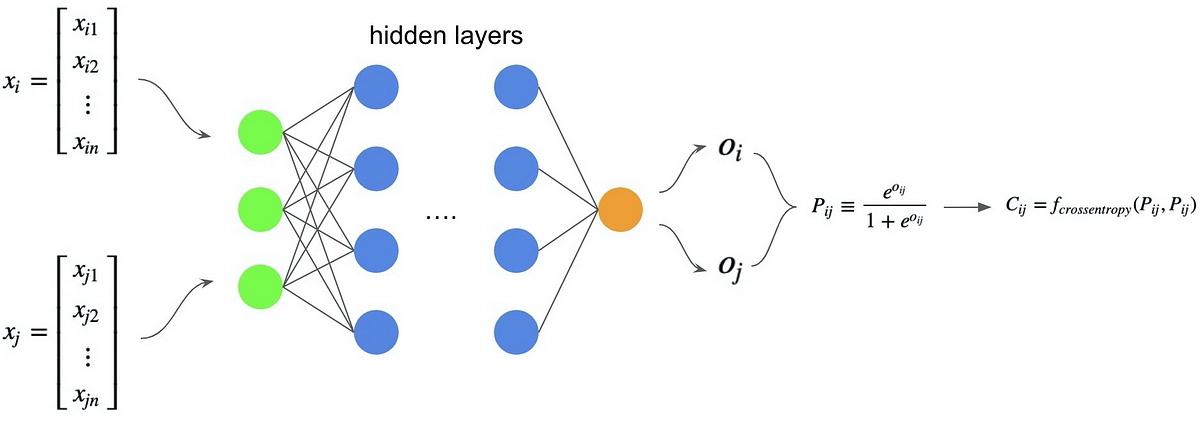
RankNet能够对文档 \(x\)输出一个打分 \(s\)，推理时直接根据打分排序

$$ s = f(x; w) $$

训练时，根据得分计算一次检索中，两个文档之间的偏序概率, \(\sigma\)是超参数：

$$ P_{ij} = P(x_i \triangleright x_j) = \frac{1}{1 + \exp(-\sigma \cdot (s_i - s_j))} $$

再定义交叉熵损失函数：

$$ C_{ij} = -\hat{P}_{ij} \log P_{ij} - (1 - \hat{P}_{ij}) \log(1 - P_{ij}) = \frac{1}{2} (1 - S_{ij}) \sigma \cdot (s_i - s_j) + \log \left\{1 + \exp(-\sigma \cdot (s_i - s_j))\right\} $$

其中 \(S_{ij} \in {-1,0,+1}\)表示文档真实关系

就可以通过梯度下降训练参数：

$$ w_k \rightarrow w_k - \eta \frac{\partial C_{ij}}{\partial w_k} $$

改进

原版RankNet的问题是一次检索产生的pair数量是 \(O(n^2)\)的，导致计算效率很低。本节介绍如何将单次检索作为一个minibatch进行一次梯度下降，这不仅仅是工程技巧，也是后续升级list-wise算法的基础。

先看结论，对一次检索产生的训练集 \(I\)（包含label不同的doc的集合，每个pair仅包含一次，且 \(\forall (i,j) \in I, S_{ij}=1\)）这次检索产生的产生的累计梯度

$$ \frac{\partial C}{\partial w_{k}} =\sum_{i} \lambda_{i} \frac{\partial s_{i}}{\partial w_{k}} $$

其中

$$ \lambda_{i} \coloneqq \sum_{j:(i, j) \in I} \lambda_{i j}-\sum_{k:(k, i) \in I} \lambda_{k i} $$

$$ \lambda_{i j} \coloneqq \frac{\partial C_{i j}}{\partial s_{i}} $$

简化的核心是利用 \(\lambda_{ij}\)的对称性

$$ \lambda_{i j} =\frac{\partial C_{i j}}{\partial s_{i}} =\sigma\left(\frac{1}{2}\left(1-S_{i j}\right)-\frac{1}{1+e^{\sigma\left(s_{i}-s_{j}\right)}}\right) = -\frac{\partial C_{i j}}{\partial s_{j}} $$

及因式分解

$$ \begin{aligned} \frac{\partial C}{\partial w_{k}} &= \sum_{(i, j) \in I} \frac{\partial C_{i j}}{\partial w_{k}} \\ &= \sum_{(i, j) \in I}\left(\frac{\partial C_{i j}}{\partial s_{i}} \frac{\partial s_{i}}{\partial w_{k}}+\frac{\partial C_{i j}}{\partial s_{j}} \frac{\partial s_{j}}{\partial w_{k}}\right) \\ &=\sum_{(i, j) \in I} \lambda_{i j}\left(\frac{\partial s_{i}}{\partial w_{k}}-\frac{\partial s_{j}}{\partial w_{k}}\right) \\ &=\sum_{i} \left(\sum_{j:(i, j) \in I} \lambda_{i j}-\sum_{k:(k, i) \in I} \lambda_{k i}\right) \frac{\partial s_{i}}{\partial w_{k}} \\ &=\sum_{i} \lambda_{i} \frac{\partial s_{i}}{\partial w_{k}} \\ \end{aligned} $$

简化后的每一项结果是与候选doc一一对应的，其中 \(\frac{\partial s_{i}}{\partial w_{k}}\)完全由模型结构和参数决定，没什么变化。而对于给定的URL \(U_1\)，其对应的λ值来自所有其他具有不同标签、针对同一查询的URL的贡献。这些λ值还可以被解释为力（在一个保守力场中，力可以表示为势能函数的负梯度）：如果 \(U_2\) 比 \(U_1\) 更具相关性，则 \(U_1\) 将受到大小为 \(|\lambda|\) 的向下推力（并且 \(U_2\) 受到相同大小的向上推力）；如果 \(U_2\) 不如 \(U_1\) 具相关性，则 \(U_1\) 将受到大小为 \(|\lambda|\) 的向上推力（并且 \(U_2\) 受到相同大小的向下推力）。

LambdaRank

RankNet做到了只考虑相对质量，但是并不侧重头部结果，只解决了问题1，仍留有问题2。以下图为例，浅灰色条代表与查询不相关的网址，深蓝色条代表与查询相关的网址。左边配对错误总数为13。右边通过将排名靠前的网址向下移动三个等级，将排名靠后的相关网址向上移动五个等级，配对错误总数减少到11个，错误总数似乎减少了。然而，像 NDCG 强调前几位结果的 IR 指标反而变差了。左边的（黑色）箭头表示 RankNet 梯度（随配对错误数的增加而增加），而我们真正想要的是右边的红色箭头。

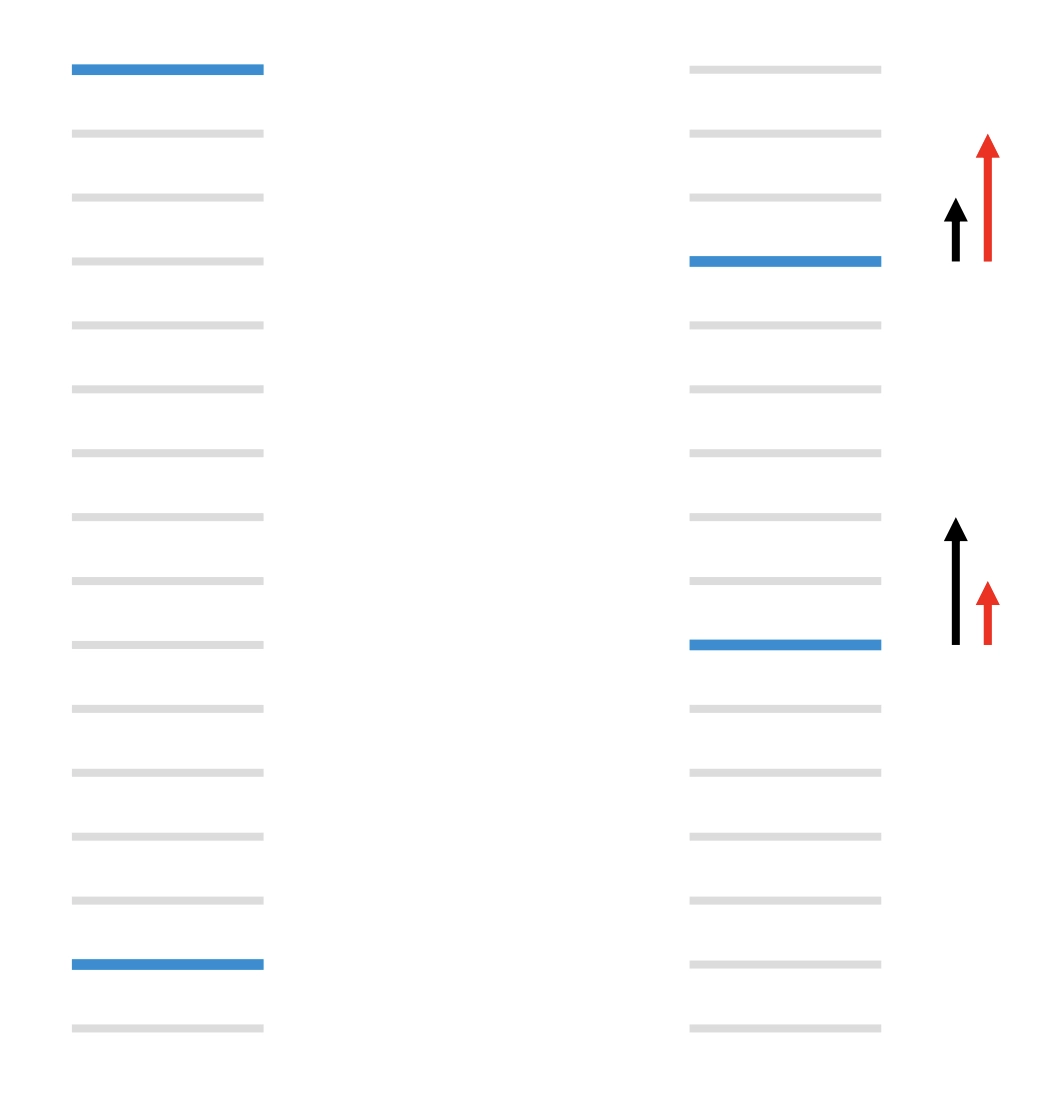
我们真正想要的是直接优化NDCG的模型。 为了训练模型，我们并不必要计算Loss本身（设计合适的损失函数是很难的）——我们只需要梯度。上面提到的箭头（ \(\lambda\)）正是那些梯度。

实验表明，通过将 \(\lambda\) 简单地乘以NDCG变化量的大小（由交换 \(U_1\) 和 \(U_2\) 的排名位置得到的 \(|\Delta_{NDCG}|\) ）能够给出非常好的结果。因此，在LambdaRank中，我们可以想象存在一个效用 \(C\) ，使得

$$ \lambda_{ij} = \frac{\partial C(s_i - s_j)}{\partial s_i} = \frac{-\sigma}{1+e^{\sigma(s_i-s_j)}} |\Delta_{NDCG}| $$

由于这里我们要最大化 \(C\)，所以对参数的更新被替换为

$$ w_k \rightarrow w_k + \eta \frac{\partial C}{\partial w_k} $$

这样就有

$$ \delta C = \frac{\partial C}{\partial w_k} \delta w_k = \eta \left(\frac{\partial C}{\partial w_k}\right)^2 > 0 $$

因此，虽然信息检索指标被视为模型得分的函数，并且处处平坦/不连续，但LambdaRank的想法通过计算排序后的URL的梯度绕过了这个问题。尽管缺乏理论基础，这一梯度对NDCG的优化效果还是被实验验证了。事实上，如果我们想优化其他的一些信息检索衡量标准，如MRR或MAP，那么LambdaRank唯一要做的变化是上述中的 \(|\Delta_{NDCG}|\) 换成其他评价指标。

LambdaMART

基本原理

梯度提升决策树有以下别名

• MART - 多重增量回归树（Multiple Additive Regression Tree）
• GBDT - 梯度渐进决策树（Gradient Boosting Decision Tree）
• GBRT - 梯度渐进回归树（Gradient Boosting Regression Tree）

MART目标是找到一个函数 \(f(x)\)，使得

$$ \hat f(x) = \text{arg min}_{f(x)} E\Bigl[L\bigl(y, f(x)\bigr) \big| x\Bigr] $$

同时MART是一个加法模型

$$ \hat f(x) = \hat f_M(x) = \sum_{m = 1}^M f_m(x) $$

模型训练过程就是不断添加新的树，假设我们已经迭代了 \(m\) 次，得到了 \(m\) 颗决策树。第 \(m+1\) 轮拟合的目标是求解：

$$ \delta \hat{f}_{m+1} = \hat{f}_{m+1} - \hat{f}_m = f_{m+1} $$

迭代目标是要在进行第 \(m+1\) 轮拟合之后降低损失函数，即：

$$ \delta L_{m+1} = L((x, y), \hat{f}_{m+1}) - L((x, y), \hat{f}_m) < 0 $$

考虑到：

$$ \delta L_{m+1} \approx \frac{\partial L((x, y), \hat{f}_m)}{\partial \hat{f}_m} \cdot \delta \hat{f}_{m+1}, $$

若取：

$$ \delta \hat{f}_{m+1} = -g_{m} = -\frac{\partial L((x, y), \hat{f}_m)}{\partial \hat{f}_m}, \tag{2} $$

则必有 \(\delta L_{m+1} < 0\)。总之，MART通过拟合负梯度更新模型参数，从而不断减小损失函数。

MART需要一个梯度，LambdaRank又恰恰定义了一个梯度，两者珠联璧合。于是Lambda+MART=LambdaMART。LambdaMART有着许多优秀特性：

• 绕过Loss定义，用梯度直接优化排序指标（如 NDCG），这些指标通常是针对整个列表计算的，与用户体验一致。
• 模型结构是GBDT，继承了决策树的优点，不易过拟合、极端值不敏感、快速训练等

LambdaMART算法流程

1. Set parameters:

   • Number of trees: \(N\)
   • Number of training samples: \(m\)
   • Number of leaves per tree: \(L\)
   • Learning rate: \(\eta\)

2. Initialization:
   For \(i = 0\) to \(m\):

   • \(F_0(x_i) = \text{BaseModel}(x_i)\)

3. Tree Building Loop:

• For \(k = 1\) to \(N\):

  • For \(i = 0\) to \(m\):
    • \(y_i = \lambda_i\)
    • \(w_i = \frac{\partial y_i}{\partial F_{k-1}(x_i)}\)
  • End for
  • Partition the data into \(L\) leaves: \({R_{lk}}_{l=1}^L\)
  • Compute leaf values:
    • \(\gamma_{lk} = \frac{\sum_{x_i \in R_{lk}} y_i}{\sum_{x_i \in R_{lk}} w_i}\)
  • Update model:
    • \(F_k(x_i) = F_{k-1}(x_i) + \eta \sum_{l} \gamma_{lk} I(x_i \in R_{lk})\)

• End for

PS: 更多细节推荐阅读材料