悬崖问题 Sarsa算法 VS Q-Learning算法 编程对比

本文用python训练一个智能体，可以从起点走向终点而不会掉下悬崖，实现并对比强化学习中的Sarsa和Q-learning算法，讨论形成最优解因素。

import numpy as np
import random

#初始化
gamma=1
#目标值函数
V=np.zeros(shape=(4,12))

S=[(i,j) for i in range(4) for j in range(12)]
#行为空间
A=list(range(4))
Q={s:[0]*4 for s in S}

start=(3,0)
terminals=[(3,11)]
cliffs=[(3,i) for i in range(1,11)]

def take_action(s,a):
    move=[(1,0),(0,1),(-1,0),(0,-1)]
    new_i=s[0]+move[a][0]
    new_j=s[1]+move[a][1]
    if 0<=new_i<4 and 0<=new_j<12:
        s_=(new_i,new_j)
    else:
        s_=s
    
    #坠崖
    if s_ in cliffs:
        return -100,start
    return -1,s_

ε-Greedy

$$ \pi(a \mid s)\left\{\begin{array}{ll} \epsilon / m+1-\epsilon & \text { if } & a^{*}=\arg \max _{a \in A} Q(s, a) \\ \epsilon / m & \text { otherwise } \end{array}\right. $$

在代码实现时，先判定如果\(X<1-\epsilon,X \sim \mu(0,1)\),直接返回最优行为，否则等概率进行选择。这样写与上式是等价的，但是编码更方便。

def epsilon_greedy(s,epsilon=0.1):
    a=np.argmax(Q[s])
    if random.uniform(0,1)<1-epsilon:
        return a
    else:
        return random.choice(A)

Sarsa

$$ Q(S,A) \leftarrow Q(S,A)+\alpha (R+ \gamma Q(S',A')-Q(S,A)) $$

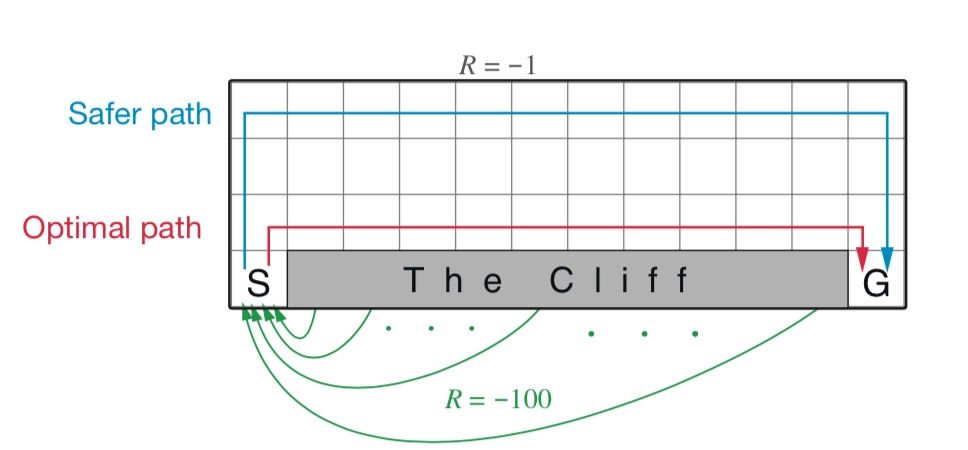
Sarsa 是一种 同策略（on-policy） 算法，它优化的是它实际执行的策略，它直接用下一步会执行的动作去优化 Q 表格。同策略在学习的过程中，只存在一种策略，它用一种策略去做动作的选取，也用一种策略去做优化。所以 Sarsa 知道它下一步的动作有可能会跑到悬崖那边去，它就会在优化自己的策略的时候，尽可能离悬崖远一点。这样子就会保证，它下一步哪怕是有随机动作，它也还是在安全区域内。

def Sarsa(n=10000,alpha=0.01):
    for i in range(n):
        s=random.choice(S)
        a=epsilon_greedy(s)
        while s not in terminals:
            r,s_=take_action(s,a)
            a_=epsilon_greedy(s_)
            Q[s][a]+=alpha*(r+gamma*Q[s_][a_]-Q[s][a])
            s=s_
            a=a_
#结果
ε=0.00001
[['↓' '↓' '→' '→' '↓' '→' '→' '→' '↓' '→' '↓' '↓']
 ['→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '↓']
 ['→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '↓']]

ε=0.1
[['→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '↓']
 ['→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '↓']]

 ε=0.5
 [['→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '↓']]

Q-learning

$$ Q(S,A) \leftarrow Q(S,A)+\alpha (R+ \gamma \max_a Q(S',A')-Q(S,A)) $$

Q学习是一种 异策略（off-policy） 算法。如图 3.31 所示，异策略在学习的过程中，有两种不同的策略：目标策略（target policy）和行为策略（behavior policy）。
目标策略是我们需要去学习的策略，一般用 \(\pi\) 来表示。目标策略就像是在后方指挥战术的一个军师，它可以根据自己的经验来学习最优的策略，不需要去和环境交互。
行为策略是探索环境的策略，一般用 \(\mu\) 来表示。行为策略可以大胆地去探索到所有可能的轨迹，采集轨迹，采集数据，然后把采集到的数据“喂”给目标策略学习。而且“喂”给目标策略的数据中并不需要 \(a_{t+1}\) ，而 Sarsa 是要有 \(a_{t+1}\) 的。行为策略像是一个战士，可以在环境里面探索所有的动作、轨迹和经验，然后把这些经验交给目标策略去学习。比如目标策略优化的时候，Q学习不会管我们下一步去往哪里探索，它只选取奖励最大的策略。

def Q_learning(n=10000,alpha=0.01):
    for i in range(n):
        s=random.choice(S)
        while s not in terminals:
            a=epsilon_greedy(s)
            r,s_=take_action(s,a)
            Q[s][a]+=alpha*(r+gamma*max(Q[s_])-Q[s][a])
            s=s_
#结果
 ε=0.1
[['→' '↓' '↓' '→' '→' '↓' '→' '→' '→' '↓' '→' '↓']
 ['→' '→' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓']
 ['→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '↓']]
 ε=0.5
 [['↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓']
 ['↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓' '↓']
 ['→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '→' '↓']
 ['↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '↑' '→' '↓']]

结果讨论

Sarsa和Q-learning都能收敛到一条从起点到终点的路径。但显然Sarsa不能总是给出全局最优解，并且ε越大，收敛结果越差。这是由于Sarsa算法中到达S’后使用ε-greedy决定下个行为，因此在悬崖边的节点很容易掉进悬崖，导致其目标值函数被低估。而在Q-learning算法中，始终选择下一个节点的最优行为更新Q值，不存在上述问题。

Sarsa 是一个典型的同策略算法，它只用了一个策略 \(\pi\)，它不仅使用策略 \(\pi\) 学习，还使用策略 \(\pi\) 与环境交互产生经验。如果策略采用 \(\varepsilon\) -贪心算法，它需要兼顾探索，为了兼顾探索和利用，它训练的时候会显得有点“胆小”。它在解决悬崖行走问题的时候，会尽可能地远离悬崖边，确保哪怕自己不小心探索了一点儿，也还是在安全区域内。此外，因为采用的是 \(\varepsilon\)-贪心 算法，策略会不断改变（\(\varepsilon\) 值会不断变小），所以策略不稳定。

Q学习是一个典型的异策略算法，它有两种策略————目标策略和行为策略，它分离了目标策略与行为策略。Q学习可以大胆地用行为策略探索得到的经验轨迹来优化目标策略，从而更有可能探索到最佳策略。行为策略可以采用 \(\varepsilon\)-贪心 算法，但目标策略采用的是贪心算法，它直接根据行为策略采集到的数据来采用最佳策略，所以 Q学习 不需要兼顾探索。