关于回测过拟合的简单介绍

量化交易中，上线的策略表现远不及预期可以说是最令人困扰的问题。本文的目的是让读者初步了解“回测过拟合”的定义、成因与几种可能的解决思路。

问题定义

什么是回测（backtest）

如果设计一种基于演绎的策略，比如利用交易规则套利，那么并不需要回测。而如果要设计基于归纳历史市场规律的策略，就需要让策略在历史环境中模拟交易，评估性能。而本文中的回测进一步缩小了讨论范围：研究者跑策略回测是为了在候选策略池中选择最佳策略。

例如，我设计了一种动量策略：“全仓持有股票池中过去W日上涨幅度最大的股票”。但是我想知道W应该怎么选取。一次典型的回测是，取W=5，10，15分别在2012-2022年的数据上模拟交易。这里选择夏普比作为性能指标。

策略编号	W	\(SR_{IS}\)
1	5	0.4
2	10	1.1
3	15	0.8

我观察到W=10的时候，SR最好，那就取W=10实盘上线。这一模型评估与选择的过程，称为回测。

什么是回测过拟合（backtest overfit）

实际上往往遇到回测失效的情况：通过调整参数让模型在历史数据上跑出很高的夏普比简单，真的实盘能赚钱很难。

一般来说， \(E[SR_{OOS}]<SR_{IS}\) (IS表示样本内，OOS表示样本外)，回测出的SR在未来数据中衰减得厉害，原因有很多，市场pattern变化、模型方差太高等等。但这里我们只考虑策略选择导致的overfit，也就是说，虽然未来的期望收益没有那么好，甚至大家都亏得厉害，但是如果 \(S_2\) 依然是其中表现最好的策略，那么这次回测就算是圆满成功。如果选出的 \(S_2\) 在未来表现垫底，就说明做回测导致我亏了更多钱，还不如随机选一只策略呢。

策略编号	W	\(SR_{IS}\)	\(SR_{OOS}\)	\(Rank_{IS}\)	\(Rank_{OOS}\)
1	5	0.4	?	1	?
2	10	1.1	?	3	?
3	15	0.8	?	2	?

根据上述想法，引出回测过拟合的定义：根据历史表现在候选池中选出的最佳策略在未来排名处于下半区。

$$ E[Rank_{OOS, selected}] < K/2 $$

K为候选策略个数。

回测过拟合的概率(probability of backtest overfitting, PBO)是

$$ P(Rank_{OOS, selected} < K/2 | Rank_{IS, selected} = K) $$

Backtest overfit与机器学习中overfit定义的最大不同之处在于，机器学习改变模型的参数，而回测只是在不同模型中选择。二者共性在于，提升样本内性能指标，导致样本外性能退化。

问题分析

原因

为什么会出现回测过拟合？上述的选择方法就是哪个策略历史夏普比高，就选谁，这可能也是被使用得最多的方法。这隐含了一个假设，就是 \(SR_{IS}\) 与 \(SR_{OOS}\) 至少是正相关的，但实际上两者可能是无关甚至负相关的。原因有两点：多重测试和环境改变。

第一，只要我做的实验足够多，总能找到在历史数据（train、val、test）上表现良好的策略。而这样被选出来的策略在未来一定是表现糟糕了。这样的行为也被称为多重测试或p-hacking。如果是刷一个光鲜的结果就是目的，利用一下选择偏差也无可厚非，但在面向实践回测中刻意使用多重测试就殊为不智了。

第二，未来金融数据和历史数据不是独立同分布的。与监督学习中出现overfit是因为模型过度学习了训练集导致模型方差太大不同的是，策略失效更类似于强化学习模型不能在另一种环境中发挥性能，是泛化能力不行。策略可能非常好地契合了当时的“真实模型”，只是这种“真实模型”在未来改变了。

一个最理想的回测系统是能够将策略获利所依赖的规律分为会在未来复现的部分，和再也不会出现的部分，这样就能精准判断其泛化性能，但这显然是一个比设计出一定赚钱的策略更难的问题，不现实。退而求其次，我们希望回测能够在策略池中选出尽量好的模型，至少不要因为模型选择多亏钱。最好还能输出PBO，以及模型未来性能衰减程度的估计值。

与机器学习算法结合

因为机器学习算法需要对历史数据进行学习，训练模型参数，所以这部份用于训练的数据不能用来评估模型。回测是对算法输出的模型进行评估，是test集的位置。如果用2010-2018的数据训练（包括train和valid），就应该用2019之后的数据做回测。

几种问题解决思路

传统方法

从统计学的角度来看，如果一个策略的SR足够高，那么这个发现是显著的。但是考虑到多做实验会增加发现高SR的概率，所以要把标准提高：一次实验SR=2就认为策略有效，做了十次实验就要求SR=3，这时SR=2的策略被认为是随机性导致的。类似的方法还有限制住总的尝试次数，要求拉长回测时间等等。这些调整阈值的办法能且只能解决多重测试带来的回测过拟合。

组合对称交叉验证

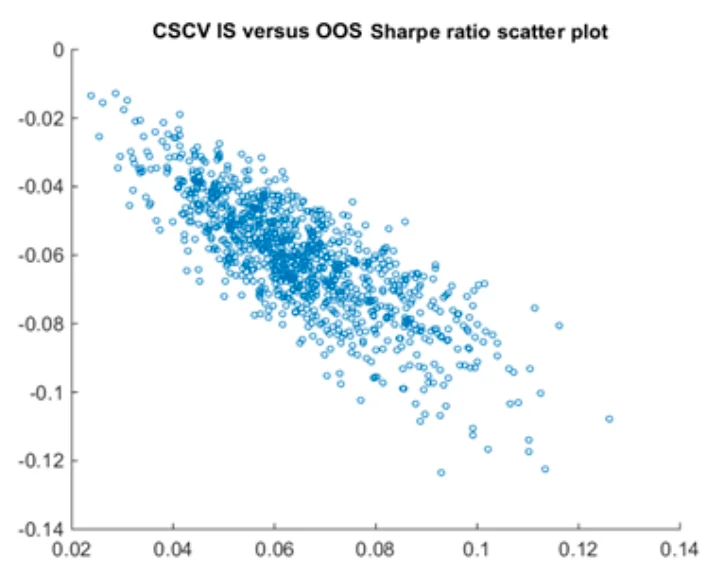
组合对称交叉验证（CSCV）的想法是，把模型选择的过程重复一万次，统计一下回测过拟合的频率，作为PBO的期望，顺便还能算出 \(SR_{IS}\) 和 \(SR_{OOS}\) 的关系。具体方法是花式切分数据集，模拟通过样本内表现选策略的过程。

CSCV把收益矩阵 \(R^{T \times K}\) 分成S个块，一半作为模拟的IS数据 \(R^{T/2 \times K}\) ，另一半作为模拟的OOS数据 \(R^{T/2 \times K}\) 。一共有 \(C_S^{S/2}\) 种组合，就重复了这么多次模型选择的过程。如果这么多次选择中， \(Rank_{IS}\) 和 \(Rank_{OOS}\) 没什么关系，就说明在这些候选模型中产生回测过拟合的概率很高。再统计一下 \(SR_{IS}\) 与 \(SR_{OOS}\) 的关系，作为对未来最佳策略性能衰减的预估。

CSCV的缺点是只能对一组候选策略算出一个PBO，不能对单个策略作出评价。而且它对于 \(SR_{IS}\) 与 \(SR_{OOS}\) 关系的预测明显是有偏的：考虑一组平均回报率相同的策略，每次在IS上选出的最佳策略，OOS上的表现一定不佳。要想使 \(Rank_{IS,best}\) 和 \(Rank_{OOS,best}\) 接近，就必须有一支策略在整个数据集上稳定优秀。我以为CSCV本质上是用一种新的算法对阈值进行调整。

贝叶斯推断

贝叶斯推断的想法是，用随机变量对回测过程建模，根据回测数据计算这些随机变量的后验分布。有了这些参数的后验分布，就可以生成新的同分布的数据，PBO、haircut之类的想知道的信息就都能算出来了。

一个最naive的模型是，假设收益矩阵的每一行都服从多元正态分布。

$$ R_t=[r_{t,1},r_{t,2}...r_{t,K}] \sim N(\mu,\Sigma) $$

用MCMC估计出 \(\mu\) 和 \(\Sigma\) 的分布，生成一万组新的数据，模拟一万次模型选择的过程，就能统计出PBO、haircut等指标。

对上述模型改进，引入隐变量 \(\gamma \sim Ber(p)\) 指示策略是不是真实发现：

$$ R_t=[r_{t,1},r_{t,2}...r_{t,K}] \sim N(\mu^*,\Sigma)\\ \mu^*_i=\gamma_i \mu $$