从 Chatterjee 相关系数到 tau-star：独立性检验的完备性与功效

在前文 《衡量序列相关性的三个指标》 中我们介绍了能够发现变量间非线性、非单调关联的Chatterjee相关系数。它形式简单，计算快速，尤其适用于筛选非线性机器学习的输入特征。然而，新的研究表明，对于部分非函数依赖情形它的检测效率存在不足。本文首先回顾并展开介绍 Chatterjee’s \(\xi\) 的具体原理和关键特性。最后介绍一种同样一致的、无需参数的独立性检验算法 \(\tau^*\) 作为替代方案。

Chatterjee相关系数回顾

定义

在考虑相关性时，我们使用术语相关性度量 (correlation measure) 来指代总体参数，术语相关系数 (correlation coefficient) 指代样本统计量，并带下标 \(n\)。符号 \(F\) 表示所考虑的随机变量对 \((X^{(1)}, X^{(2)})\) 的联合二元分布函数，\(F_1\) 和 \(F_2\) 分别是各自的边缘分布函数。

令 \((X_{[1]}^{(1)}, X_{[1]}^{(2)}), \dots, (X_{[n]}^{(1)}, X_{[n]}^{(2)})\) 是样本的一个重排，使得 \(X_{[1]}^{(1)} \le \dots \le X_{[n]}^{(1)}\)。如果 \(F_2\) 是连续的，再假设\(X_1^{(2)}, \dots, X_n^{(2)}\) 之间不相等（实践中影响较小，本文不作考虑），那么 \(r_{[i]}\) 是 \(X_{[i]}^{(2)}\) 在 \(X_{[1]}^{(2)}, \dots, X_{[n]}^{(2)}\) 中的秩。

定义 Chatterjee相关系数 \(\xi_n\) 为

$$\xi_n = 1 - \frac{3 \sum_{i=1}^{n-1} |r_{[i+1]} - r_{[i]}|}{n^2 - 1}.$$

直观的理解是，Chatterjee相关系数衡量顺序排列 \(X^{(1)}\) 后，相邻的 \(X^{(2)}\) 是否相近。

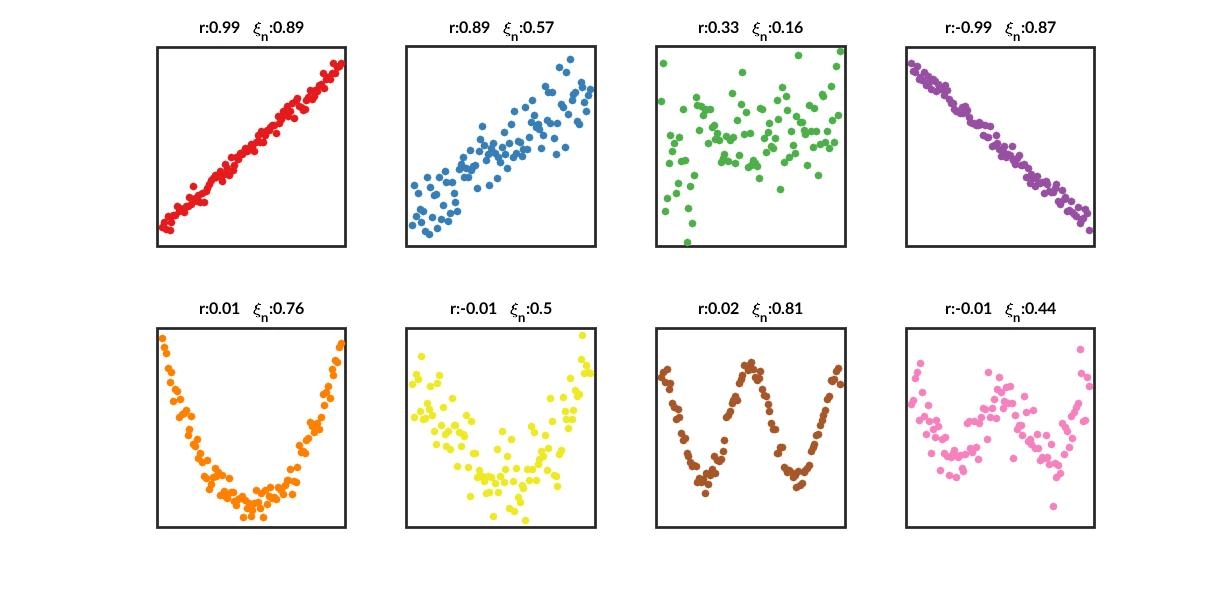
Chatterjee (2021) 证明了 \(\xi_n\) 估计了 Dette-Siburg-Stoimenov 秩相关度量

$$\xi = \frac{\int \operatorname{Var}(E[I(X^{(2)} \ge x) \mid X^{(1)}]) dF_2(x)}{\int \operatorname{Var}(I(X^{(2)} \ge x)) dF_2(x)}.$$

这个式子长得很像决定系数 \(R^2\)，即 \(\frac{\text{Explained Variance}}{\text{Total Variance}}\)（可解释方差 / 总方差）。其实本质上确实就是决定系数，但它是在一个更广泛、更普遍的非参数框架下定义的：把“用 \(X^{(1)}\) 预测 \(X^{(2)}\) ”这件事，拆成“对所有阈值 \(x\) 的二分类问题”，再把每个二分类的“可解释方差占比”做平均。

把 \(X^{(2)}\) 固定阈值成二元标签 \(Y_x=\mathbf{1}{X^{(2)}\ge x}\)。 \(E[Y_x\mid X^{(1)}]\) 是”在给定 \(X^{(1)}\) 时，\(X^{(2)}\) 超过阈值 \(x\) 的条件概率“。

对任意随机变量都有全概率方差分解

$$ \operatorname{Var}(Y_x)=\underbrace{E\big[\operatorname{Var}(Y_x\mid X^{(1)})\big]}_{\text{不可解释噪声}} +\underbrace{\operatorname{Var}\big(E[Y_x\mid X^{(1)}]\big)}_{\text{被 }X^{(1)}\text{ 解释}} $$

\(\operatorname{Var}(E[Y_x\mid X^{(1)}])\) 衡量”这个条件概率在不同 \(X^{(1)}\) 取值上有多大起伏“。起伏越大，说明 \(X^{(1)}\) 确实在改变超过阈值的概率，预测力越强。

分母 \(\operatorname{Var}(Y_x)=p_x(1-p_x)\) 是该二分类任务本身的”基线”。\(\xi\) 最后对所有阈值 \(x\) 做积分（用 \(F_1, F_2\) 加权），相当于对全体分位点平均。

$$ \xi = \frac{\displaystyle \int \underbrace{\operatorname{Var}\big(E[\mathbf{1}\{X^{(2)}\ge x\}\mid X^{(1)}]\big)}_{\text{被 }X^{(1)}\text{ 解释的部分（跨 }X^{(1)}\text{ 的差异）}} dF_2(x)} {\displaystyle \int \underbrace{\operatorname{Var}\big(\mathbf{1}\{X^{(2)}\ge x\}\big)}_{\text{总方差（阈值 }x\text{ 下的基线不确定性）}} dF_2(x)} $$

特性

这个度量 \(\xi\) （及其样本估计量 \(\xi_n\)）之所以在现代统计学中备受关注，是因为它具有以下几个革命性的特性：

关键特性1：捕捉非线性和非单调关系

传统的 Pearson \(\rho\) 只能捕捉线性关系。Spearman \(\rho\) 或 Kendall \(\tau\) 只能捕捉单调（同增同减）关系。 \(\xi\) 的优势: \(\xi\) 可以检测到任何类型的函数关系，包括非单调关系（如 U 型 \(Y = X^2\)）或更复杂的关系。比如对于 \(Y = X^2\) (其中 \(X \sim U(-1, 1)\))，Pearson 和 Spearman 相关系数都接近 0，但 \(\xi\) 会趋向一个正值，正确地表明 \(Y\) 完全依赖于 \(X\)。

关键特性2：不对称性

Pearson, Spearman 和 Kendall 都是对称的：\(\rho(X, Y) = \rho(Y, X)\)。

\(\xi\) 是不对称的。

• \(\xi(X^{(1)}, X^{(2)})\) 度量的是 \(X^{(1)} \to X^{(2)}\) 的依赖程度。
• \(\xi(X^{(2)}, X^{(1)})\) 度量的是 \(X^{(2)} \to X^{(1)}\) 的依赖程度。

这两个值通常不相等。\(\xi\) 允许量化这种单向的、类似因果推断的预测强度。

关键特性3：方便好算

用到的是指示函数 \(\mathbf{1}{X^{(2)}\ge x}\) 与分布函数 \(F\) 的积分，对任意单调变换不敏感，天然稳健。不设模型，完全非参数。

把样本按 \(X^{(1)}\) 排序后，顺序扫一遍就能累计这些”相邻 \(X^{(2)}\) 的“跳变度”，实现上能做到 \(\mathbb{O}(n\log n)\) 复杂度，用numpy两三行就能搞定。

理论完美与实践功效不足

Chatterjee (2021) 提出的相关系数 \(\xi_n\) 之所以引起轰动，在于其总体度量 \(\xi\) 还具有一个革命性的理论特性：\(\xi=0\) 当且仅当两个变量 \(X^{(1)}\) 和 \(X^{(2)}\) 相互独立。这使其在理论上成为一个“完备”的独立性度量，优于只能捕捉线性关系（Pearson \(\rho\)）或单调关系（Spearman \(\rho\)）的传统系数。

然而，Shi et al. (2021) 指出，尽管 \(\xi\) 的理论定义完美，但基于其样本统计量 \(\xi_n\) 的独立性检验，在统计功效（Statistical Power）上存在严重不足。即 \(\xi_n\) 在“是否独立”的检验上是 一致但不高效 的，尤其在某些局部依赖下几乎失灵。

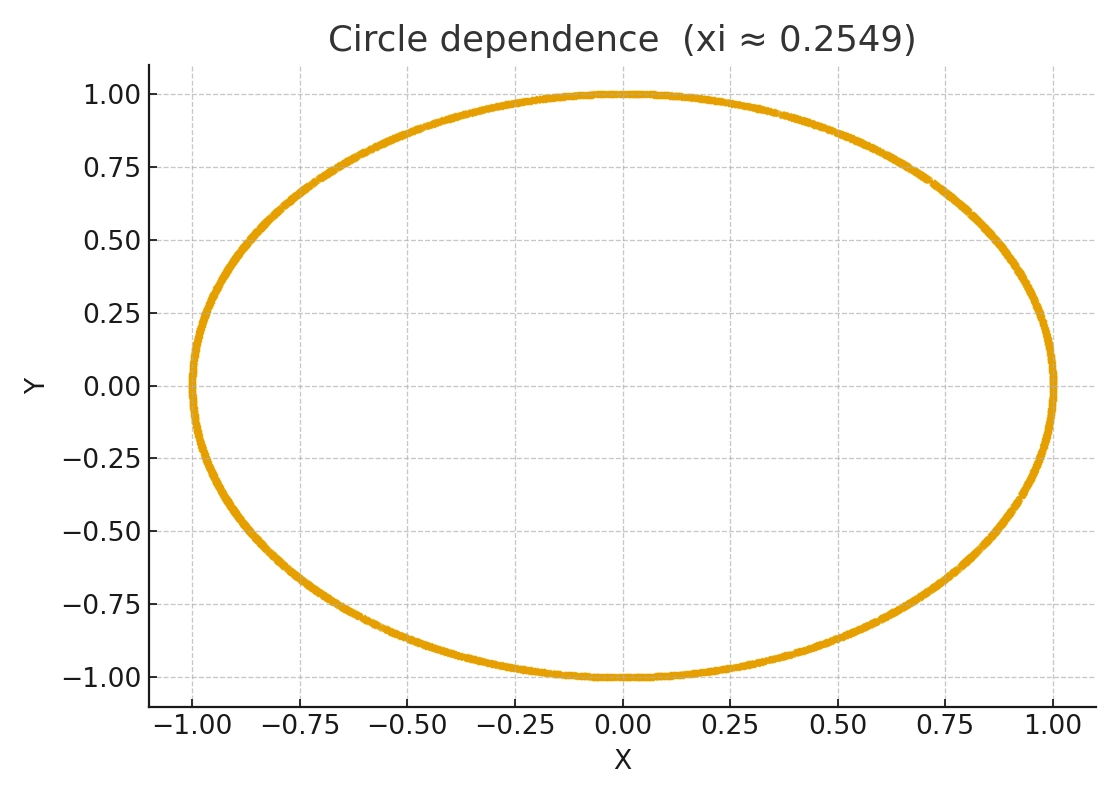
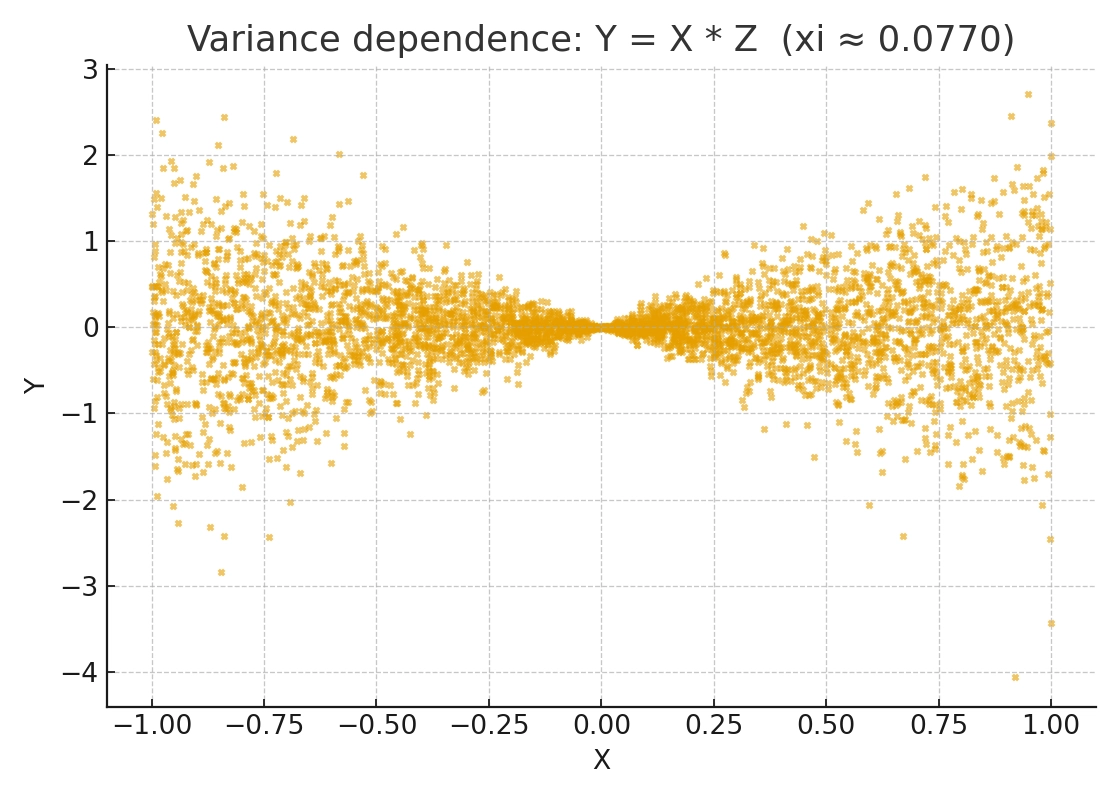
这个缺陷可以从两个层面来理解。

数值信号弱（有限样本表现）

\(\xi\) 本质上度量的是条件期望 \(E[I(X^{(2)} \ge x) \mid X^{(1)}]\) 跨越 \(X^{(1)}\) 时的“起伏”。对于某些特定的依赖类型，例如对称的非单调关系（如 U 形、圆环）或纯粹的异方差依赖，这个“起伏”本身可能非常小，甚至被抵消。

因此，对于这些“形状依赖”，其理论真值 \(\xi\) 虽然大于 0，但数值可能极其微小。在有限样本中，这个微弱的信号 \(\xi_n\) 很容易被噪声淹没，导致观测值“看起来像 0”。这不是因为 \(\xi\) 理论上等于 0，而是因为信号太弱且 \(\xi_n\) 向这个微小真值的收敛速度很慢。

渐近功效低（统计检验的灵敏度）

这种对特定形状的“信号迟钝”直接导致了其在统计检验中的致命弱点。论文通过“局部功效分析”证明了这一点。

当设置一个依赖关系非常微弱的“局部备择假设”（即依赖强度随样本量 \(n\) 以 \(n^{-1/2}\) 速率衰减）时，\(\xi_n\) 检验的统计功效会完全崩溃。论文的定理1指出，在这种情况下，\(\xi_n\) 检验的功效趋近于 \(\alpha\)（即检验的显著性水平，如 5%）。

这意味着，\(\xi_n\) 检验在面对微弱信号时，其表现与“盲猜”无异；它无法区分微弱的真实依赖和纯粹的随机噪声。

相比之下，Hoeffding’s \(D\)、Blum-Kiefer-Rosenblatt’s \(R\) 和 Bergsma-Dassios’s \(\tau^*\) 等经典系数，在相同的微弱信号下仍能保持“速率最优”（rate-optimal），即它们依然具有非平凡的功效，能够灵敏地检测到这种依赖。

并非独立性的万能检测器

Shi et al. (2021) 证明了 \(\xi_n\) 是速率次优 (rate sub-optimal) 的。尽管 \(\xi_n\) 理论定义优雅、计算高效 (\(O(n \log n)\))，但如果用于检验独立性这一核心目的，它是一个不够灵敏的工具。在实践中看到一个很小的 \(\xi_n\) 值，我们无法断定变量是真独立，还是存在一个 \(\xi_n\) 无法有效检测到的非函数式或弱依赖关系。

凡是不独立的特征，理论上就包含可预测的信息——它在统计上是“有价值”的。从机器学习角度，不独立等于潜在可预测性。在量化投资中 \(\xi_n\) 的这一局限往往意味着一个对风险有预测能力的特征被错杀。

同样基于秩关系的独立性检验tau-star

\(\tau^*\)（tau-star）是 Bergsma & Dassios (2014) 提出的一个一致性独立性检验统计量，它是 Kendall’s τ 的推广版本，它更适合做严肃的独立性检验，而 \(\xi_n\) 更适合作为高效的非线性特征筛选统计量

Kendall’s τ 定义为：

$$ \tau = E[\operatorname{sign}(X_1 - X_2)\operatorname{sign}(Y_1 - Y_2)] $$

它反映了两点对的 一致（concordant）与不一致（discordant）概率差。但 τ 在某些非单调依赖下可能为 0，即使 X 与 Y 并不独立，因此检验不一致。

定义：

Bergsma 与 Dassios 在此基础上定义了一个新相关性度量：

$$ \tau^* = E[a(X_1, X_2, X_3, X_4)a(Y_1, Y_2, Y_3, Y_4)] $$

其中 \(a\) 是一种基于四元组的”符号协方差”函数。

$$ a(z_1, z_2, z_3, z_4) = \operatorname{sign}\left(|z_1 - z_2| + |z_3 - z_4| - |z_1 - z_3| - |z_2 - z_4|\right) $$

样本统计量：

$$ t^* = \frac{1}{\binom{n}{4}} \sum a(x_i,x_j,x_k,x_l)\,a(y_i,y_j,y_k,y_l) $$

在连续情形下（无 ties），该度量满足：

$$ \tau^* \ge 0 \quad \text{且} \quad \tau^* = 0 \iff X, Y \text{ 独立} $$

因此它给出了一个 一致（consistent）独立性检验。

\(\tau\) 对应两点的”是否同向变化”；
\(\tau^*\) 则考察 四点的联合相对顺序。

定义四点组 \(({(x_1,y_1),…,(x_4,y_4)})\)：

• 若可被一个坐标轴划分，使得两对点在 X 与 Y 上顺序一致或都反向，则称”四点一致（concordant quadruple）”；
• 若一对一致一对不一致，则称为”四点不一致（discordant quadruple）”。

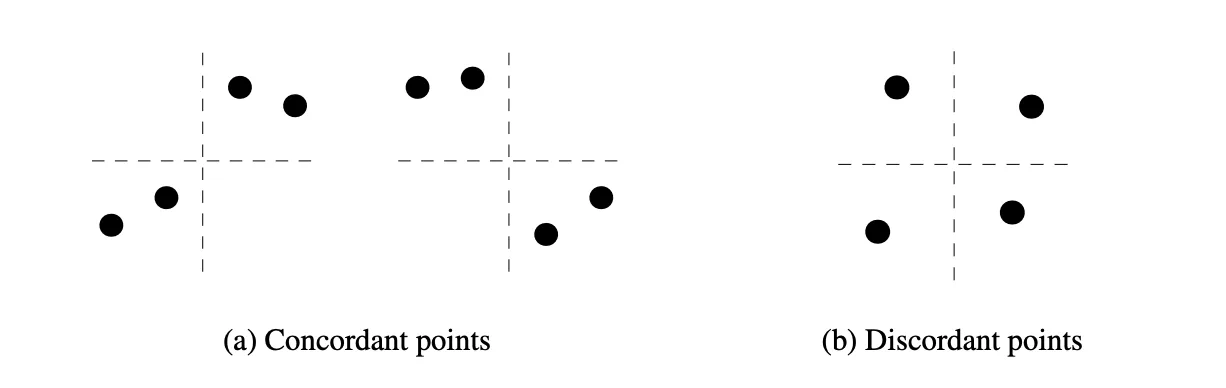
Bergsma & Dassios 证明：

$$ \tau^* = \frac{2P(\text{四点一致}) - P(\text{四点不一致})}{3} $$

且在独立情形下，四点一致概率 \((=1/3)\) ，不一致概率 \((=2/3)\) 。一旦 \(X,Y\) 之间存在任何规律（线性、曲线、周期、环形），四个点的相对顺序分布就偏离独立情形，四点一致的概率上升，导致 \(\tau^* > 0\) 。

在实践中，使用 \(\tau^*\) 进行独立性检验是通过置换检验 (Permutation Test)来实现的。

若要将 \(\tau^*\) 用作 0 到 1 之间的依赖性度量，可以使用归一化版本：

$$ \tau_b^* = \frac{\tau^*(X, Y)}{\sqrt{\tau^*(X, X) \tau^*(Y, Y)}} $$

\(\tau_b^* \in [0,1]\)，1 对应“函数关系（无噪声）”。

总结

Chatterjee 相关系数 \(\xi_n\) 把“用 \(X\) 预测 \(Y\)”拆成对所有阈值的二分类任务，从

$$ \operatorname{Var}\big(P(Y\ge x\mid X)\big) $$

这个角度刻画预测力。对应的总体量 \(\xi\) 满足 \(\xi=0 \iff X\perp Y\)，对函数型依赖（包括非单调）有 \(\xi=1\)，表达力上是“完备”的；同时 \(\xi_n\) 只需 \(O(n\log n)\) 算法，在大样本特征筛选中非常适合作为非线性、非单调相关性的快速打分指标。

问题在于：Shi–Drton–Han 表明，在某些对称/方差依赖的局部备择下，\(\xi\) 的真值本身非常接近 0，且 \(\xi_n\) 对 \(n^{-1/2}\) 级别的微弱依赖几乎“无感”，渐近功效退化到显著性水平 \(\alpha\)，属于 rate sub-optimal。所以，\(\xi_n\) 虽然是一致的独立性检验统计量，但并不是一个高功效的“万能独立性检测器”。

Bergsma–Dassios’s \(\tau^*\) 则改用四元组的相对顺序作为秩信息，在连续情形下满足

$$ \tau^* \ge 0,\quad \tau^* = 0 \iff X\perp Y, $$

对任意依赖关系给出一致检验，并在局部备择下达到 速率最优，代价是计算更复杂。

因此，实践上的合理分工是：

• \(\xi\) 非线性特征快速筛选
• \(\tau^*\) 严肃检验“是否独立”、尤其关注风险建模时

相关性统计量的对比

指标	线性/单调	任意依赖	分布无关	局部功效\((n^{-1/2})\)	计算
Pearson \(\rho\)	线性	否	否	次优	极快
Spearman/Kendall	单调	否	部分	次优	快
\(\xi\)	函数化（含非单调）	原则上可	是	次优（对称/非单调类）	快 \(O(n\log n)\)
\(\tau^{*}\)	任意	是	是	最优	优化后 \(O(n\log n)\)

---

参考文献

• Bergsma, Wicher, and Angelos Dassios. 2014. “A Consistent Test of Independence Based on a Sign Covariance Related to Kendall’s Tau.” Bernoulli 20 (2). https://doi.org/10.3150/13-BEJ514.
• Chatterjee, Sourav. 2021. “A New Coefficient of Correlation.” Journal of the American Statistical Association 116 (536): 2009–22. https://doi.org/10.1080/01621459.2020.1758115.
• Shi, H, M Drton, and F Han. 2022. “On the Power of Chatterjee’s Rank Correlation.” Biometrika 109 (2): 317–33. https://doi.org/10.1093/biomet/asab028.