神经网络与截面资产定价——先验的艺术

本文讨论了在实证截面资产定价领域，如何结合金融先验设计深度学习模型，具体包括预测目标设计、市场环境建模与网络结构选择三部分。

引言

“没有免费午餐”（NFL）定理是机器学习的基本原理——在不结合具体问题的情况下，讨论机器学习算法优劣是没有意义的，所有算法能力可看作是一致的。从贝叶斯理论视角来看，之所以在具体问题上某些算法表现更佳，是因为这些算法内在假设更符合真实场景。不同的模型结构、训练方法、损失函数都可视作人类引入的先验知识，结合真实数据样本后（训练过程），我们可以计算后验概率。在数据给定的情况下，最终模型效果很大程度上取决于人们的先验知识是否正确，以及是否合适地在建模中体现，机器学习算法是先验的艺术。如CNN隐含空间平移不变性的先验知识，使计算机视觉领域迈入新的时代。

量化投资领域，GBDT类算法（xgboost/lightgb/etc）在股价预测这样的中等数据量、高噪声数据集上表现优异，鲁棒性强，简单地构造若干层神经网络效果是难望其项背的。既然如此，为何还需要深度学习模型预测截面收益率呢？原因仍在于先验。决策树的集成无法直接建模股票市场的时空结构，或是考虑因子动量和市场情绪，而借助神经网络结构的灵活性，我们可以引入对这些对象的建模，与GBDT形成互补。下表整理了一些金融理论、建模对象和神经网络结构的关系，后文将展开论述。

金融理论	建模对象	网络结构
多因子理论	预测目标	Loss
因子动量、市场情绪	市场环境	Gating/extra feature
无效市场假说	时序信息	RNN/LSTM/GRU/Attention
公司间关联	空间信息	GCN/GAT/Hyper Graph/Attention

预测目标

神经网络模型的训练是由损失函数梯度的反向传播实现的，损失函数Loss的定义直接决定了神经网络的预测目标及隐含假设。如均方误差MSE假定误差服从高斯分布，是回归任务的常用损失函数，也经常用于截面收益率预测。但细究之下，使用MSE学习单个资产预期收益率并不符合因子定价理论。第一，在定价理论和因子投资实务中，我们并不关心资产的绝对表现，而是只关注相对表现，只需要找出相对最佳的资产即可，不涉及对市场整体走势预测。第二，即使将标签替换为相对收益，由于市场的时变特性，假定一个相同的高斯分布还是有问题的。

因此收益率模型的损失函数应借鉴排序学习的思想，将每一期视作一个query，候选资产视作document，构造一个list-wise的损失函数，如相关系数IC。在此额外介绍CCC Loss，这是同时考虑截面相关性和个体误差的一个损失函数，定义是，

$$ CCCL_{x,y} = 1- \frac{2\sigma_{xy}}{\sigma^2_x+\sigma^2_y+(\mu_x-\mu_y)^2} $$

有等价形式

$$ CCCL_{x,y} = 1-\frac{2\sigma_{xy}}{2\sigma_{xy}+MSE_{x.y}} $$

CCC 最初是情感识别中常用的指标，用于衡量真实情感维度与预测情感程度之间的一致性。如果预测值发生了偏移，分数将根据偏差进行惩罚。因此，CCC 比皮尔森相关性、MAE 和 MSE 更可靠地评估维度语音情感识别的性能。从其等价形式可以看出它同时考虑了截面相关性和MSE。

收益率预测同时包含了方向和幅度，如果只考虑幅度无视方向，那么就是风险模型。我们往往需要一个稳定的、由一组正交风险因子\(\mathbf{F}\)定义的风险模型。2021年由微软提出的DRM（Deep Risk Model）旨在通过设计损失函数，通过监督学习方法直接得到风险模型。其损失函数定义为

$$ \min _{\theta} \frac{1}{T} \sum_{t=1}^{T}\left[\frac{1}{H} \sum_{h=1}^{H} \frac{\left\|\mathbf{y} \cdot, \mathbf{t}+\mathbf{h}-\mathbf{F}_{\cdot t}\left(\mathbf{F}_{\cdot t}^{\top} \mathbf{F}_{\cdot t}\right)^{-1} \mathbf{F}_{\cdot t}^{\top} \mathbf{y} \cdot \mathbf{t}\right\|_{2}^{2}}{\left\|\mathbf{y}_{\cdot, \mathbf{t}+\mathbf{h}}\right\|_{2}^{2}}+\lambda \operatorname{tr}\left(\left(\mathbf{F}_{\cdot t}^{\top} \mathbf{F}_{\cdot t}\right)^{-1}\right)\right] $$

式子第一项是最大化经验\(R^2\)

$$ R_{\cdot t}^{2}=1-\frac{\left\|\mathrm{y} \cdot t-\mathbf{F}_{\cdot t}\left(\mathbf{F}_{\cdot t}^{\top} \mathbf{F} \cdot t\right)^{-1} \mathbf{F}_{\cdot t}^{\top} \mathbf{y} \cdot t\right\|_{2}^{2}}{\|\mathbf{y} \cdot t\|_{2}^{2}} $$

为了避免挖掘出大量相似度极高的因子，作者通过限制方差膨胀系数(VIF)，使得因子尽量正交。经过推导，作者给出VIF等价形式，构成式子的第二项

$$ \Sigma \text{}{VIF}_i = N \cdot tr((F^TF)^{-1}) $$

最后作者定义问题为对未来N天解释度的多目标优化，从而使得风格因子有极高的自相关性。

可见通过设计损失函数我们可以在监督学习范式中还原多因子定价理论的本义，在截面上学习资产收益率差异，最终生成收益率模型和风险模型。

市场环境

现有研究表明，不同市场环境下投资者的乐观/悲观情绪会造成因子性能变化，如熊市中低波动等“防守型”因子往往表现更好。此外，因子动量全球市场上显著，因子表现存在自相关性。以上两点全局信息无法通过“point-wise”的特征引入，需要设计显式的模型结构。

实践上，最简单的处理方式是把全局信息向量化，与资产特征向量拼接，作为弱特征，这在九坤kaggle大赛中被证明有效。

$$ x' = m \sqcap x $$

此外，通过门控机制调整因子权重也是很自然的想法。

$$ x' = g(m) \odot x $$

最后市场信息也可以被引入混合专家模型的路由选择、注意力机制的query。理论上，通过数据驱动的市场环境感可以知帮助模型在全周期取得更佳表现，但也对数据量和正则化方法提出了更高要求。

时空结构

GBDT从模型层面对所有样本一视同仁，不考虑资产间关联关系，即“空间结构”。而从金融理论上出发，市场中存在“动量溢出”效应，关联企业间收益率存在领先-滞后关系。这种关联源于投资者的有限注意力，信息没有瞬时反应在相似企业上，而是随时间扩散。下表展示了一些已知的关联类型。

文献	效应
Hou (2007)	行业动量（intra-industry effect）
Cohen and Frazzini (2008)	重要客户动量（supplier-customer effect）
Cohen and Lou (2012)	复杂公司动量（conglomerate lead-lag effect）
Lee et al. (2019)	科技关联度（technological links）
Parsons, Sabatucci and Titman (2020)	地理动量（geographic lead-lag effect）
Ali and Hirshleifer (2020)	分析师共同覆盖（shared analyst coverage）

从深度学习模型结构角度来看，这种关联关系适用图神经网络——将公司视为节点，关联关系视为邻边/超边，聚合相似股票特征。

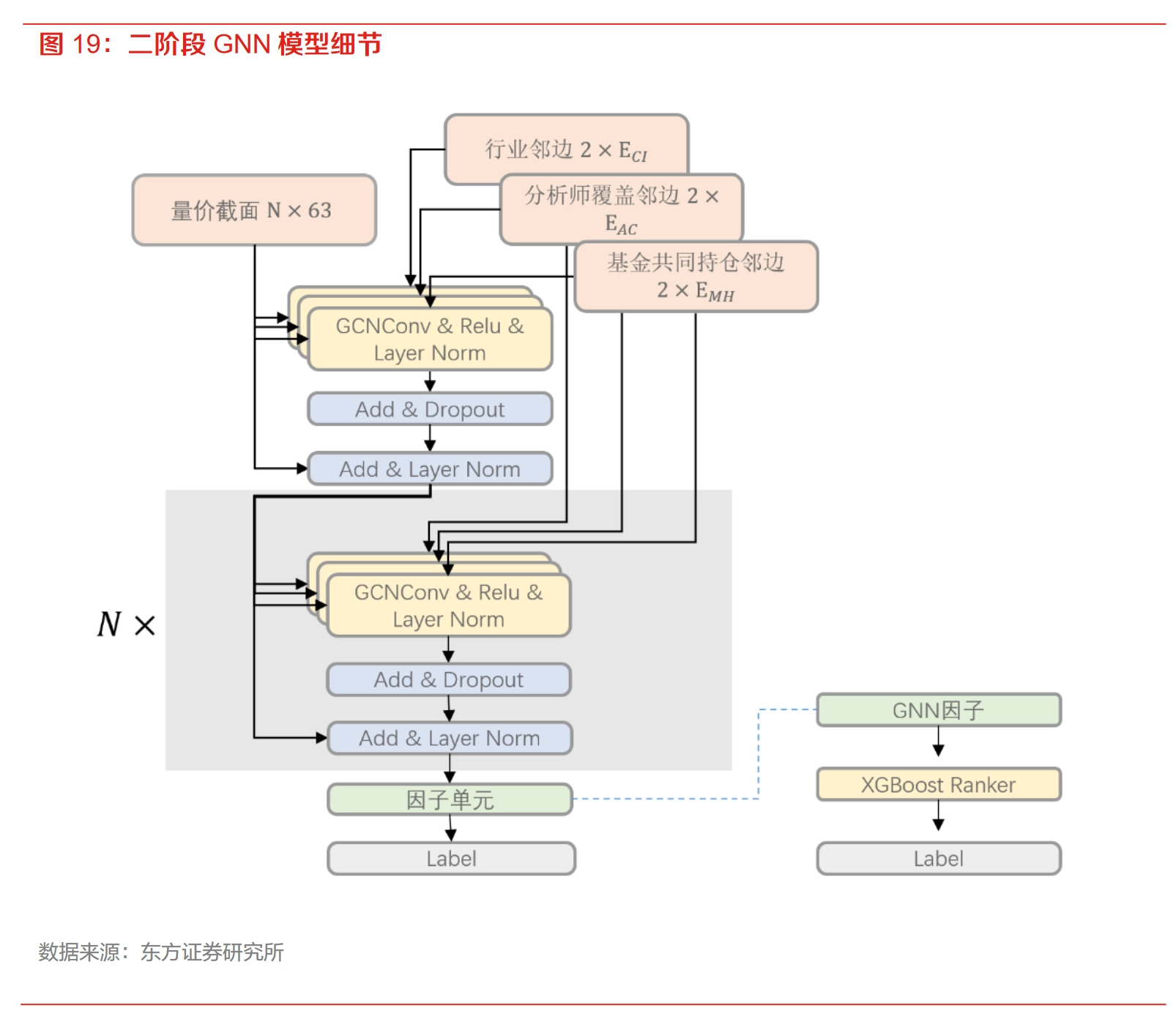
由于截面上股票数量规模并不大，所以也可以用Transformer的核心模块多头自注意力机制计算全量的关联关系。此时股票间关联完全由数据驱动，无需人工定义，关联信息可以通过特征引入，隐式建模。如AAAI2024中MASTER网络在时间和空间上都使用了Attention建模。

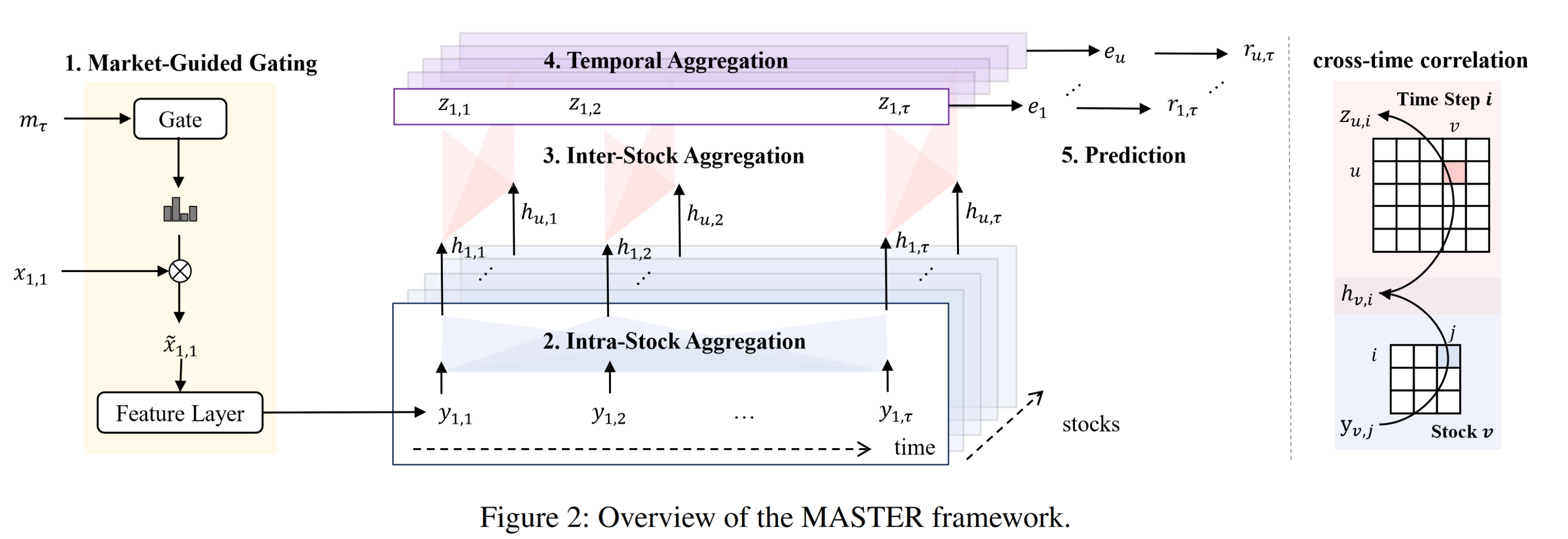
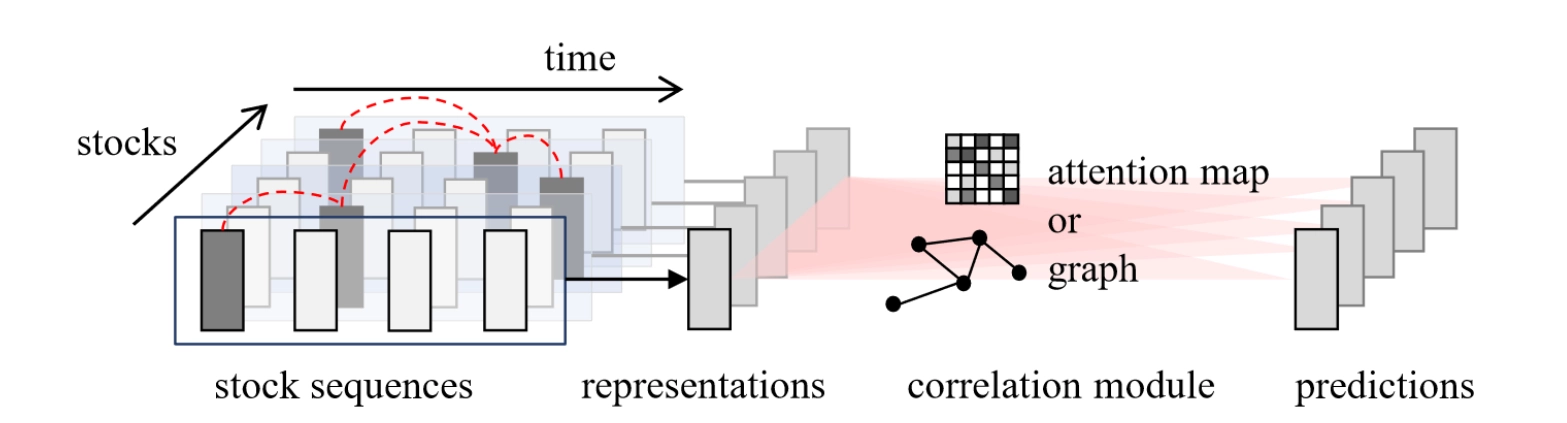
在时间上，考虑资产特征向量序列也能对预测有所提升，已有工作大多使用时序信息抽取+空间建模+最终预测的三阶段结构。在提取时序信息的网络结构上，成熟且常用的是LSTM、GRU等循环神经网络，也可以使用Attention机制。

总结

本文相信在资产定价领域，纯粹的数据驱动方法是无法取得成功的，任何有效模型都应该是特定人工先验与数据的结合。研究者应更多从金融先验出发，将深度学习模型从玄学炼丹的桎梏中解放。