股票日内高频波动的十四行诗：度量与分解

Sonnet of Intraday Stock Volatility: Metrics and Decomposition.

本文讨论了股票日内高频波动的若干度量，并在统一视角下总结了其多种分解方法，为波动率相关的投资实务提供参考。

度量

矩

假设股票的对数价格满足以下跳跃-扩散模型（Jump-Diffusion Model）:

$$ dp_t = \mu p_t dt + \sigma p_t dW_t + J_t dp_t $$

\(dp_t\) 是股票价格的变化,\(\mu\) 是扩散部分的年化平均收益率,\(\sigma\) 是股价扩散部分的波动率,\(dW_t\) 是布朗运动的随机微分项,\(J_t\) 是跳跃的随机微分项，表示跳跃事件的影响。

著名的已实现波动率（Realized Variance）度量了日内股价波动率大小，它依概率收敛于积分波动率与日内对数价格跳跃之和。

$$ \sum_{i=1}^{N} r_{i}^{2} \stackrel{\mathcal{P}}{\rightarrow} \int_0 ^T \sigma_s^2 d s+\sum_{0 \le \tau \leq T}\left(\Delta p_{\tau}\right)^2 $$

如果考虑高阶矩，我们可以更进一步地度量日内收益分布的形态和非对称性。日内收益率的已实现x阶矩(Realized Moment x)定义为：

$$ RM_{x}=N^{x/2-1} \frac{\sum_{i=1}^{N} r_{t, i}^{x}}{R V_{t}^{x / 2}} $$

已实现偏度因子RM3是由高频数据描述的收益率不对称性，因子值为负时表示高频收益率存在左偏，此时较高的预期收益是对左偏的补偿；另外一般认为日内有极端正收益的股票会引发非理性投资者的博彩偏好，因此因子为正时预期超额收益为负。因子总体方向负向。

已实现峰度因子RM4是由高频数据描述的收益率峰态与尾部形态。因子值较低时对应尾 部重尾现象不明显，即尾部风险较小，倾向于有更好的预期表现，在逻辑上其因子 方向亦为负。

超偏度RM5类似于偏度，描述了不对称性；而超尾度RM6类似于峰度，描述了峰态以及尾部与中心的相对信息。但二者对于尾部的积分权重更大，更深刻的描述了尾部风险。

尾部风险

描述尾部风险的风险度量有在险价值(Value at risk; VaR)和条件在险价值(cVaR/Expected shortfall)。VaR是在特定分位点（如5%，95%）对应的股票收益率，cVaR则是分位点外侧的期望收益率。相比上述的中心矩因子，VaR/cVaR聚焦于极端情况下的收益率分布，并且使用CVaR 进行风险度量可以更加稳健地估计可能发生的风险。

在逻辑上我们认为，尾部风险波动较小的，或者风险水平保持相对稳定的股票相对于尾部风险出现大幅波动的，或者风险水平难以估计或预测的股票更加优质，因为风险的大小和风险的变动程度反应了投资者的过度投机现象。

VOV

东北证券构造的波动率的波动率（Volatility of volatility）描述了风险的不确定性，

$$ \operatorname{VOV}_{t}=\frac{\sqrt{\frac{1}{\tau-1} \sum_{s=0}^{\tau-1}\left(R V_{t-s}-\overline{R V_{t}}\right)^{2}}}{\overline{R V_{t}}} $$

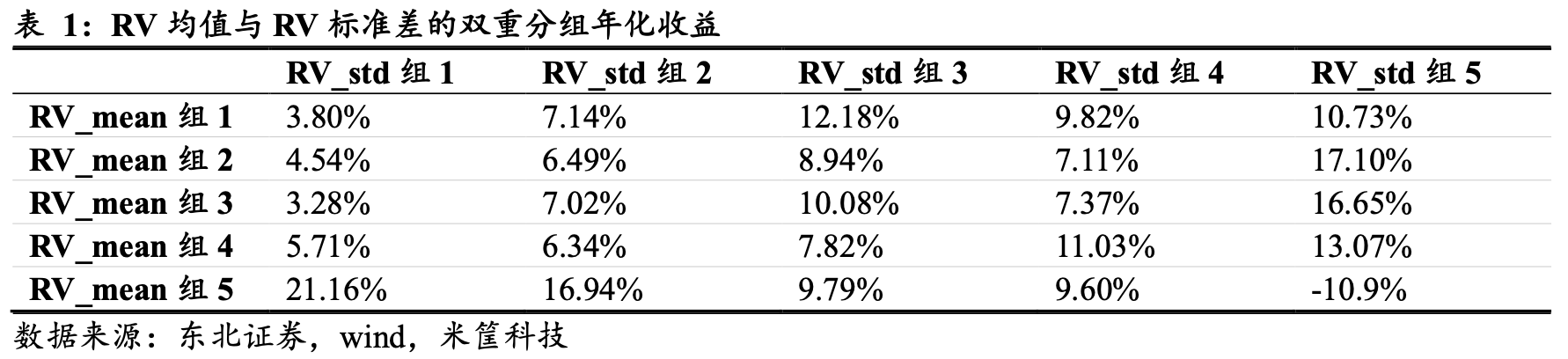
分子部分是过去一段时间已实现波动率的标准差，分母部分不仅使得因子截面可比，从双重排序来看也是对因子的增强。在高风险组内，已实现方差波动率与预期收益率负相关性更加显著，这表明对于风险处于较高水平的资产，投资者会更加关注风险自身的不确定性，VOV 效应增强。

分解

上下行分解

根据收益率的正负，可以讲已实现波动率分解为上、下行已实现波动率，并计算上下行波动率不对称性。 \(RV=RV^++RV^-\)

$$ RV^+=\sum_{i=1}^{N}{r_i^+}^2 $$

$$ RV^-=\sum_{i=1}^{N}{r_i^-}^2 $$

波动率不对称性因子，用RV归一化后即为RSJ因子。

$$ SJ={RV}^+-{RV}^- $$

$$ RSJ=\frac{SJ} {RV} $$

连续/跳跃部分分解

日内股价波动率QV=积分波动IV+跳跃波动QJ

我们可以使用通过多幂次变差估计积分波动IV

$$ \hat{IV} = \mu_{2/3}^{-3} \sum_{i=3}^{n} {|r_i|^{\frac23}|r_{i-1}|^{\frac23}|r_{i-2}|^{\frac23}} $$

其中

$$ \mu_{2/3} = 2^{1/3} \frac{\Gamma(5/6)}{\Gamma(1/2)} $$

RJV则是对QJ的估计

$$ RJV=max(RV-\hat{IV},0) $$

跳跃波动的长/短程分解

RJV=RLJV+RSJV，将高于阈值 \(\gamma\) 的收益率算作长程跳跃，反之则为短程跳跃。

$$RLJV=min(RJV,\sum_{i=1, |r_i| > \gamma}^{N}{r_i^2 i})$$

其中

$$\gamma = \alpha N^{-0.49} \sqrt{\hat{IV}}$$

多重分解

结合以上三种分解，我们可以得到上下行跳跃波动分解：

$$RJVP=max(RV^+-\hat{IV}/2,0)$$

$$RJVN=max(RV^--\hat{IV}/2,0)$$

$$SRJV=RJVP-RJVN$$

以及长短程上下行跳跃波动分解：

$$RLJVP = min(RJVP, \sum_{i=1, r_i > \gamma}^{N}{r_i^2}))$$

$$RLJVN = min(RJVN, \sum_{i=1, r_i < -\gamma}^{N}{r_i^2}))$$

$$SRLJV = RLJVP-RLJVN$$

总结与展望

本文简要介绍了度量日内股价波动率的数十个因子，主要方向是对日内高频波动总体和局部的度量、风险不确定性的度量，以及各个子成分的度量，希望对读者深入研究提供参考。虽然本文的因子较多，且在历史回测上有显著表现，但其中很多构造逻辑是相似的。如何辨析它们之间的内在联系，考察相关性，防止同时出现大幅回撤会是一个重要课题。

未来，一个显而易见的改进思路是将对数收益率全部替换为特质收益率，这在 之前的文章 中有过讨论，并且也非常有希望提升因子表现。

参考文献

• Aït-Sahalia, Yacine, 和Jean Jacod. 2012. 《Analyzing the Spectrum of Asset Returns: Jump and Volatility Components in High Frequency Data》. Journal of Economic Literature 50 (4): 1007–50. https://doi.org/10.1257/jel.50.4.1007.
• Andersen, Torben G, Tim Bollerslev, Francis X Diebold和Paul Labys. 2001. 《The Distribution of Realized Exchange Rate Volatility》. Journal of the American Statistical Association 96 (453): 42–55. https://doi.org/10.1198/016214501750332965.
• Barndorff-Nielsen, O. E. 2004. 《Power and Bipower Variation with Stochastic Volatility and Jumps》. Journal of Financial Econometrics 2 (1): 1–37. https://doi.org/10.1093/jjfinec/nbh001.
  Bollerslev, Tim, Sophia Zhengzi Li和Bingzhi Zhao. 2020. 《Good Volatility, Bad Volatility, and the Cross Section of Stock Returns》. Journal of Financial and Quantitative Analysis 55 (3): 751–81. https://doi.org/10.1017/S0022109019000097.
• Duong, Diep, 和Norman R. Swanson. 2015. 《Empirical evidence on the importance of aggregation, asymmetry, and jumps for volatility prediction》. Journal of Econometrics, Econometric Analysis of Financial Derivatives, 187 (2): 606–21. https://doi.org/10.1016/j.jeconom.2015.02.042.
• Yu, Bo, Bruce Mizrach和Norman Rasmus Swanson. 2019. 《New Evidence of the Marginal Predictive Content of Small and Large Jumps》. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.3440320.
• 20230227-东北证券-因子选股系列之四：高频数据下的已实现高阶矩因子及改进
• 20230601-东北证券-因子选股系列之五：基于高频数据的风险不确定性因子
• 20200204-方正证券-市场微观结构剖析系列1：分钟线的尾部特征
• 20220831-广发证券-高频数据因子研究系列九：基于股价跳跃模型的因子研究