量价因子的新枝——特质风险类因子初探

客云近岁花特异，往往变出呈新枝

低波动率（低风险）异象是全球二级市场中普遍存在的著名异象，而基于特质收益率计算的特质风险类（特质波动率）因子是其中的杰出代表。剔除了系统性风险因子影响后，个股的残差收益率被认为能更好地表征风险，由此构造的因子也具有更优表现。在隐式因子框架下，本文介绍了特质波动因子的理论基础、在A股市场实证以及后续改进思路。

特质波动之谜

在传统的资产定价理论中，不能被系统性风险因子解释的的特质性风险并不具备风险溢价——投资者可以通过充分的多样化消除这些风险。但从2006年特质波动率（idiosyncratic volatility, IVOL）与未来收益率的显著负相关关系被提出以来，大量实证研究支持这一现象存在，这一异象被称为“特质波动之谜”(idiosyncratic volatility puzzle)。

文献[1]从定价效率与套利不对称性角度给出了一种广为接受的解释：其一，更高的IVOL意味着更高的套利风险，使得错误定价无法被充分消除。其二，投资者对错误高估/低估的股票套利具有不对称性，高价股更难被做空。因此在全市场中，IVOL和预期收益率呈现出负相关关系。下图展示了以错误定价等级分组，越是被高估的组别中，特质波动异象就越强烈，而在低估组中，关系逆转为正相关。在A股市场中也有类似结论，不过没有出现逆转为正相关的现象。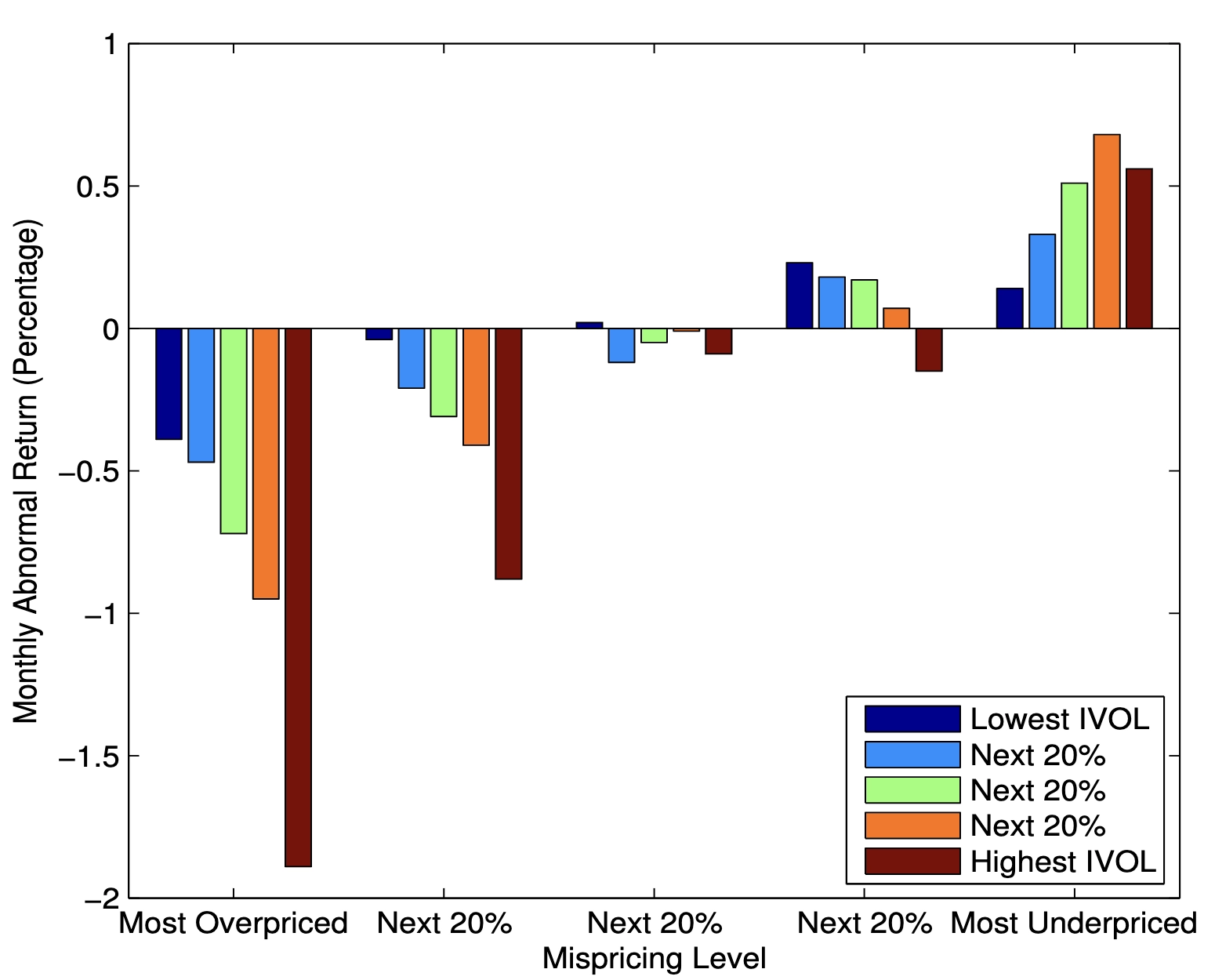

A股实证研究

隐式因子框架下的特质因子

传统的特质收益率计算方式为，用个股日频收益率对因子模型（CAPM、FF3、FF5）做回归，取残差作为特质收益率。

$$ r_{i,t} = \alpha_i + \Sigma_j{\beta_{j,t}F_{j,t}} + \epsilon_{i} $$

其中r为个股i收益率， \(\epsilon\) 为个股特质收益率（特质风险）。在这样的方法中，我们会面临选择因子模型时遗漏因子，或是解释度不强等问题，因此国信证券[2]提出了在隐式因子框架下计算特质因子。具体来说，使用主成分分析法（PCA）直接分解收益率矩阵，取前n个特征值作为系统风险因子。

日频特质类因子

隐式因子框架下的复合特质因子在 IC、ICIR 和多空收益表现上优于传统的多因子框架下的特质波动因子。此外，由于无需经过预设因子、构建模拟组合回测等过程，隐式因子框架在实际操作上也具备简洁性。

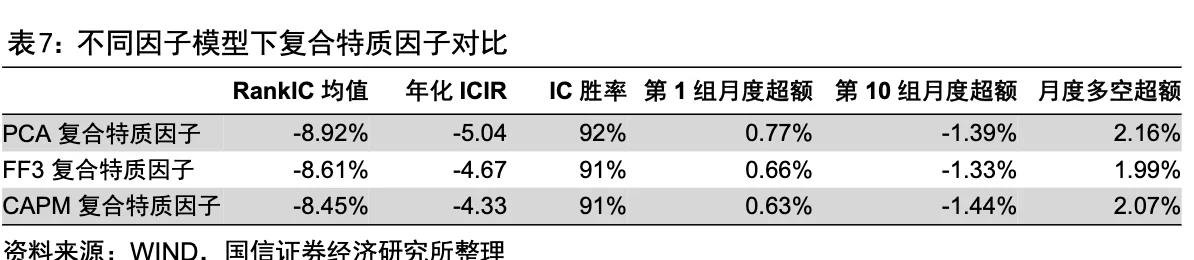
国信[2]将隐式因子框架下的特质波动、特异度、特质偏度因子等权重合成，构建了隐式因子框架下的复合特质因子。该复合特质因子的 RankIC 均值为-8.92%，年化 ICIR 为-5.04，月度胜率为 92%。第一组月均超额收益为 0.77%，第十组月均超额收益为-1.39%，多空月均超额收益为 2.16%。复合特质因子表现出非常强的预测能力和稳定性，优于单个因子，也优于显式因子框架下的 Fama-French 三因子复合特质因子。

高频特质类因子

财通证券基于5min高频数据构造特质偏度因子，RankIC 均值达到-9.5%[6]。东北证券[3]基于高频数据计算的特质收益改进风险因子（RV）与风险不确定性因子（VOV），选股表现相对于原始因子均有一定程度的提升。

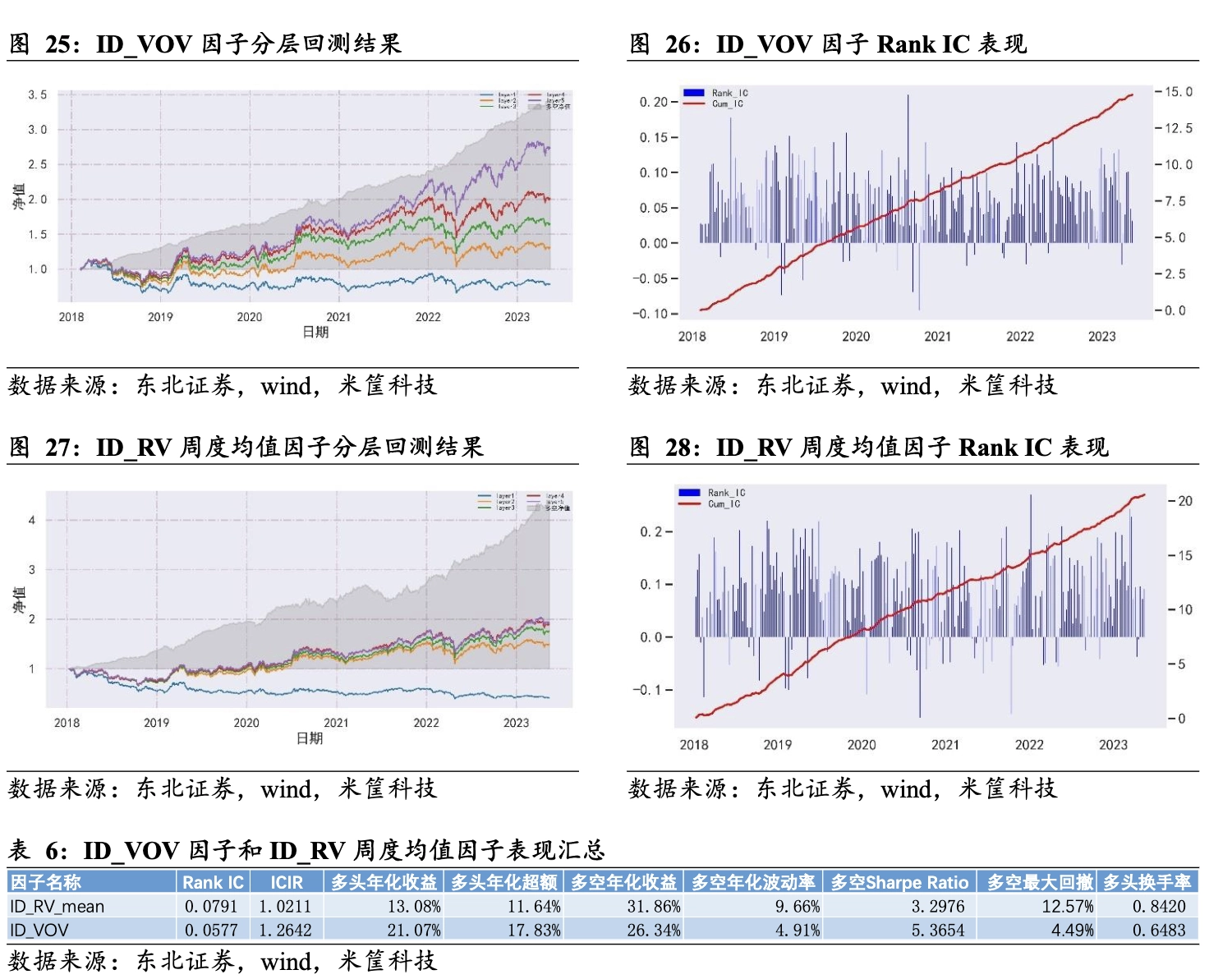
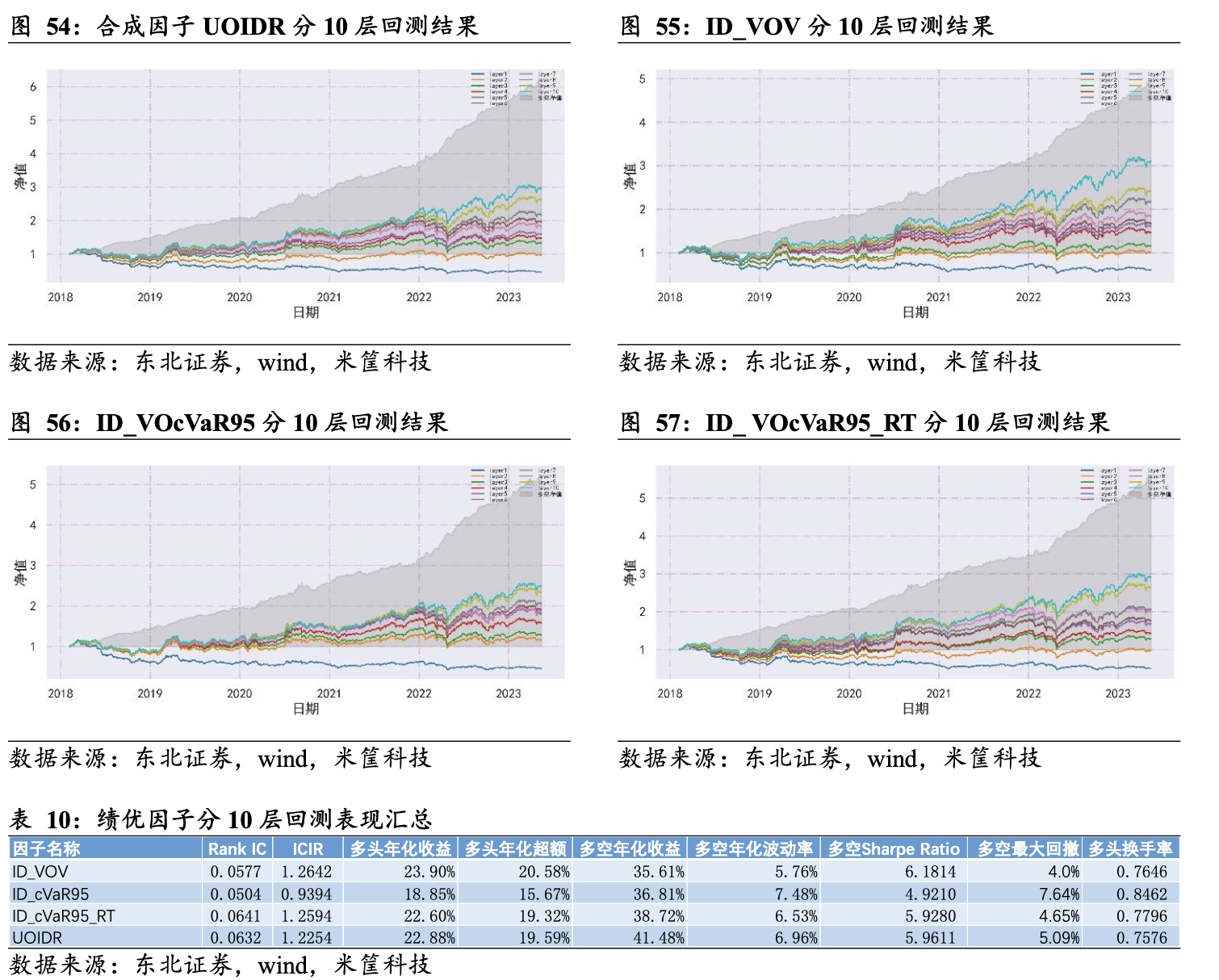
拓展与增强

波动率聚集Volatility Clustering

波动率聚集现象——学术研究表明，金融资产收益的时间序列数据，通常表现出波动率聚集现象。该现象存在于个股层面，就导致股票的波动率因子具有较强的跨期截面相关性。针对这一现象，文献[4][5]给出了截然相反的处理方式。

东吴证券认为在利用传统波动率因子进行每月选股时，由于这种相关性而被重复利用的过往因子信息，会给我们带来干扰，削弱当期因子的选股效果。给出的解决方案是每月月底将本月因子值对过去 6 个月的因子值做多元线性回归，取残差作为“纯真波动率”。结论是剔除不同阶数截面相关性后的纯真波动率因子，选股效果均优于传统的特质波动率因子。

而民生证券则是使用GARCH(1,1)模型刻画收益率序列的波动聚集性，使得估计的波动率更加可靠，用模型预估值取代历史波动率作为因子。IVOL_garch因子的表现相较IVOL取得大幅提升。检验发现，在一般市场情况下 GARCH 模型预测的特质波动率与历史特质波动率相差无几，而在市场出现大幅波动时期（特别是波动率因子出现回撤的牛市期），GARCH 模型预测的特质波动率能更精准的识别波动率的大幅变化。

定价效率中性化

国信证券将表中的定价效率修正因子复合特质因子进行截面回归，并取残差作为定价效率因子修正后的复合特质因子，因子稳定性得到提升。不过结合[1]的结论，本文认为应该考虑两者直接的非线性关系，而非简单剔除。

其他指标的特质序列

相较原始的多因子模型，主成分分析方法下对最大共同波动的提取可以不仅限于日收益序列，还可以拓展至日内收益、隔夜收益以及换手率等其他指标，并构造相应的特质波动因子

参考文献

[1.]Stambaugh, Yu和Yuan, 《Arbitrage Asymmetry and the Idiosyncratic Volatility Puzzle》.
[2.]20220817-国信证券-金融工程专题研究：隐式框架下的特质类因子改进
[3.]20230601-东北证券-因子选股系列之五：基于高频数据的风险不确定性因子
[4.]20200528-东吴证券-“波动率选股因子”系列研究（一）：寻找特质波动率中的纯真信息——剔除跨期截面相关性的纯真波动
[5.]20190520-民生证券-低波动异象：解析、改进及成因实证
[6.]20191210-财通证券-博彩偏好还是风险补偿？高频特质偏度因子全解析