2022-03-30发表2022-03-30更新数据科学

Risk of Rain 2 工程师指数流配装

Risk of Rain 2中角色DPS可以被分解为数个子项的乘积（基础攻击力、攻速、暴击率等），因此线性堆叠攻速、暴击等属性的装备数量增加可以带来指数级的dps增长。类似地，角色的坦度也可以被分解为总血量乘以护甲。由于装备资源有限、巨大的边际收益以及提升成本不一致导致的复杂性，有必要提前计算装备数量约束下达到最大DPS和有效生命的最优配装。而这对于工程师而言是最有意义的，因为炮塔是以纯粹站桩输出的形式出现的。

极限DPS

主要机制分析

base damage 基础攻击力

total damage 击中时打出的实际总伤害

触发伤害基于基础攻击力/实际伤害

proc coefficient 触发系数，比如导弹的触发系数是1，正常触发尤克里里，但尤克里里只有0.2的触发系数，每个弹射有10%*0.2=2%的概率触发导弹。

掉落概率
白装：绿装：红装=63：27：1

物品分析

不考虑击杀效果（如狂战士的肩铠）、同品质数值被完爆的装备、基于基础伤害的上限较低的装备，不考虑效果较特殊的高等级装备

攻速：黄针、掠夺本能、战争号角（假设触发）、不寻常的珍珠
暴击率：红镜、掠夺本能、不寻常的珍珠
暴击倍数：激光瞄准镜
触发伤害：导弹、带电穿孔器、熔岩穿孔器、尤克里里、粘土炸弹、辉煌巨兽
伤害倍数：精致手表（有风险）、焦点水晶、穿甲弹、不寻常的珍珠，根据Amdahl’s law弃用撬棍、老断头台等物品

数学模型

$$ DPS = Coeff \cdot BaseDamage \cdot AttackSpeed \cdot (1 + CritRate \cdot (CritDamage-1)) \cdot TriggerDamage $$

前五项比较简单：

$$ BaseDamage = 14 + 2.8lvl\\ Coeff = 1 + 0.1N_{focus} \\ CritDamage = 2 + N_{laser} \\ CritRate = min(1, 0.01 + 0.1N_{Red} + \min{(0.05,N_{instinct})} + 0.1N_{pearl})\\ AttackSpeed = 1 + 0.15N_{yellow} + 0.24N_{instinct} + 0.1N_{pearl} + min(0.7, N_{horn})\\ $$

主要考虑触发效果造成的伤害：效果会相互连续触发，且触发概率、过程系数不同。假设有导弹、尤克里里、粘土炸弹各一，一次射击会首先从三个二项式分布中采样，用向量表示三者触发的概率是$P_1=(0.1,0.25,0.05)$，之后的触发要考虑到过程系数，向下一个状态转移。比如导弹再次触发的概率是 $P_{2,1} = 0.1 * (1 * 0.1 + 0.2 * 2 * 0.25 + 0 * 0.05 ) = 0.02$，实际上这是固有触发概率0.1和上一次触发的等效攻击次数0.2的乘积。

记第n级各效果触发概率为k维向量$P_n$，效果过程系数矩阵$C$，原始触发概率矩阵$P_1$
那么有递推式

$$ P_n^{T}=C \cdot P_{n-1}^{T} \cdot P_1^T $$

$$ \sum_i { P_{n,i} \rightarrow 0 }, n \rightarrow \infin $$

并且呈指数衰减，所以可以只计算前5级的情况。

至于伤害，考虑导弹触发的导弹伤害可以达到$3^n$，有4个导弹单发伤害的数学期望就可以达到无穷大，但实际触发概率很低，也极有可能造成伤害溢出（打boss时或许有强制截断逻辑）。因此计算触发效果伤害时本文采用初始total damage的倍数作为保守估计。

最后我们求解等式约束的最优化问题

只有绿白装的情况

$$ \max _ N DPS \\ s.t. \forall N_i \in N \\ N_{focus}+N_{red}+N_{yellow}+N_{bomb} = 20 \\ N_{missle}+N_{ukulele}+N_{instinct} = 10 $$

代码

def loss(w):
    focus, red, yellow, bomb, missle, ukulele, instinct = w
    coeff = 1 + 0.1*focus
    crit_damage = 2
    crit_chance = min(1, 0.01 + 0.1*red +min(0.05,instinct))
    attack_speed = 1+0.15*yellow+0.24*instinct

    P_1 = np.array([0.1, 0.25*0.8, min(1,0.05*bomb)*1.8])
    C = np.array([1,min(1, 0.2*ukulele),0])

    P_2 = C.dot(P_1.T)*(P_1.T)
    P_3 = C.dot(P_2.T)*(P_1.T)
    P_4 = C.dot(P_3.T)*(P_1.T)
    P_5 = C.dot(P_4.T)*(P_1.T)

    missle_times, ukulele_times, bomb_times  = sum([P_1,P_2,P_3,P_4,P_5])
    missle_damage = 3*missle*missle_times
    ukulele_damage = 0.8*ukulele_times
    bomb_damage = 1.8*bomb_times

    dps = coeff * (1 + crit_chance*(crit_damage-1)) * attack_speed * (1 + missle_damage + ukulele_damage + bomb_damage)
    return -dps

cons = [{'type': 'eq', 'fun': lambda w:  sum(w[:4])-20},
        {'type': 'eq', 'fun': lambda w:  sum(w[4:])-10}]
bnds = [(0, 200)]*7

ret = minimize(loss, [1,1,1,1,1,1,1], method='SLSQP', bounds=bnds, constraints=cons)

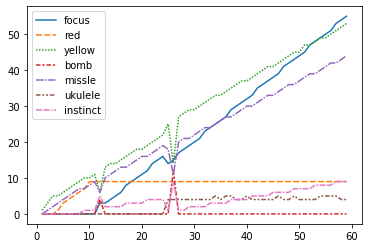
计算随着装备总数增长，最优解变化情况

结果分析： 白色装备中，前期1：1拿黄针和红镜，在红镜达到9个时，开始拿专注水晶，水晶：黄针目标数量是1：1，炸弹没用。绿色装备中，导弹全期强势，掠夺者本能后期有用，数量大概是导弹五分之一。尤克里里重要性受超参数影响较大，规律是弹射次数达到需求上限前无脑拿，它的主要输出来自触发其他效果。

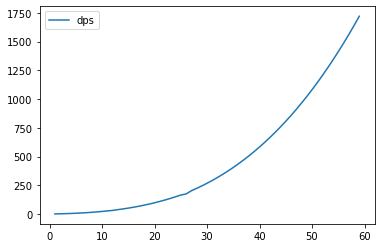
dps增长情况：随着装备数量增加，dps指数增长，每多一件装备增长13.2%左右。

借助指数增长的威力，绿白装就足以使伤害溢出了。类似地，计算引入boss装备后的最优配装。

def loss(w, lvl=10):
    (
        #白
        focus,
        red,
        yellow,
        bomb,
        steak,
        psg,
        slug,
        fungus,
        tough,
        #绿
        missle,
        ukulele,
        instinct,
        #红
        clover,
        #boss
        charged_perforator,
        molten_perforator,
        ir_pearl,
    ) = w

    coeff = 1 + 0.05 * focus + 0.1 * ir_pearl
    crit_damage = 2
    crit_chance = min(1, 0.01 + 0.1 * red + min(0.05, instinct) + 0.1 * ir_pearl)
    attack_speed = 1 + 0.15 * yellow + 0.24 * instinct + 0.1 * ir_pearl

    P_1 = np.array([0.1, 0.25 * 0.8, min(1, 0.05 * bomb) * 1.8, 0.1, 0.1])
    C = np.array([1, min(1, 0.2 * ukulele), 0, 1, 2.1])

    P_2 = C.dot(P_1.T) * (P_1.T)
    P_3 = C.dot(P_2.T) * (P_1.T)
    P_4 = C.dot(P_3.T) * (P_1.T)
    P_5 = C.dot(P_4.T) * (P_1.T)

    (
        missle_times,
        ukulele_times,
        bomb_times,
        charged_perforator_times,
        molten_perforator_times,
    ) = sum([P_1, P_2, P_3, P_4, P_5])
    missle_damage = 3 * missle * missle_times
    ukulele_damage = 0.8 * ukulele_times
    bomb_damage = 1.8 * bomb_times
    charged_perforator_damage = (
        5 * charged_perforator * charged_perforator * charged_perforator_times
    )
    molten_perforator_damage = (
        3 * 3 * molten_perforator * molten_perforator * molten_perforator_times
    )

    dps = (
        coeff
        * (1 + crit_chance * (crit_damage - 1))
        * attack_speed
        * (
            1
            + missle_damage
            + ukulele_damage
            + bomb_damage
            + charged_perforator_damage
            + molten_perforator_damage
        )
    )

    hp = (130 + 39 * lvl) * (1 + 0.1 * ir_pearl) + 25 * steak
    shield = 0.08 * hp * psg
    regen = 0.6 + 0.2 * lvl + 3 * slug + 0.045 * 2 * fungus * hp + 0.1 * ir_pearl

    Q = (1 + 0.15 * tough) ** (1 + clover)

    R1 = regen * Q
    R2 = (hp + shield) * Q
    R = np.log(R1)*np.log(R2)

    score = dps

    return -score


bnds = [(0, 50)] * 16

极限肉度

机制分析

游戏中总血量包括Health, Shield和Barrier。
获得health主要靠升级和肉排，个人护盾生成器psg可以获得shield。爆裂真菌fungus和蛞蝓slug堆回血。

血条质量包括了护甲和格挡概率。

护甲公式

$$ DamageDealt = \frac{100}{100+Armor},Armor>0 $$

$$ \frac{HP_{adjusted}}{HP} = 1 + Armor/100 $$

格挡概率

$$ BlockChance = 1-\frac{1}{1+0.15x} $$

x为“艰难时光”数量

$$ \frac{HP_{adjusted}}{HP} = 1 + 0.15x $$

可以看出单一属性对有效血量的提升都是线性的，把三者组合起来可以获得指数增长，但问题是没有能够永久加护甲的装备，所以看起来只能提升总血量+格挡率这两者，略显乏力。

但好在57叶草这件红装能给格挡概率判定带来质变：假设装备y件57叶草，单次格挡概率就变为

$$ BlockChance' = 1-(\frac{1}{1+0.15x})^{1+y} $$

等效血量对x求偏导

$$ \frac{d\frac{HP_{adjusted}'}{HP}}{dx} = (1+y)(1+0.15x)^{y} $$

此时艰难时光带来的有效血量指数增长！！！
举例来说，装备20个艰难时光，5个57叶草，此时格挡概率为99.976%, 等效血量就是基础血量的4000+倍。即使没那么多装备，10个艰难时光+2个草也能提供16倍的等效血量。事实上，如果装备200个艰难时光和25个草，命中率会低至2的-128次方，超出单精度表示范围，可能进入真正的无敌模式。

但这只是理论期望值，会不会有一下子没挡住，导致直接被秒呢？答案是前期有可能，后期不会：首先由于一击保护（OSP）的存在，血量至少会保留10%，只需要考虑此时还能抗多少下伤害。
假设此时连续受到10次至死伤害，格挡事件服从二项式分布$X \sim B(10, p’)$
全部格挡的概率由概率质量函数给出

$$ f(k,n,p')=C_n^kp'^k(1-p')^{n-k}=(1-(\frac{1}{1+0.15x})^{1+y})^{10} $$

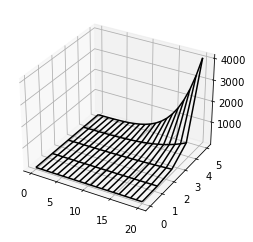
如果装备15个艰难时光，2个57叶草，成功概率为74.4%

如果装备20个艰难时光，5个57叶草，成功概率为99.8%

数学建模

“撑肉”实际上有两个优化目标，一是站桩能力，二是抗住爆发的能力。

定义站桩能力为每秒能够承受多少dps，

$$ R_1 = Regen * Q $$

抗爆发力=血条厚度*血条质量

$$ R_2=(health+barrier+shield)*Q $$

定义综合肉度

$$ R=\sqrt{R_1R_2} $$

以工程师,困难难度为讨论对象，我们要求解的问题是

$$ \max R $$

血条长度和回血：

$$ health = 130 + 39lvl + 25N_{steak} \\ shield = 0.08*health*N_{psg} \\ regen = 0.6 + 0.2lvl + 3N_{slug} + 0.045N_{fungus} \cdot health \\ $$

血条质量(不堆护甲)

$$ Q = (1+0.15N_{tough})^{1+N_{clover}} $$

数值计算的结果是，线性加数值的装备（肉排、护盾生成器等）都是辣鸡，在前期也没用，艰难时光+草是无敌的，蘑菇两个就够。

总结

引入boss装和红装的综合配装

白色输出方面，前期1：1拿黄针和红镜，红镜到9个开始补专注水晶，目标数量是黄针=专注；防御装配两到三个蘑菇，别的全拿艰难时光

绿色前期导弹、尤克里里和掠夺者本能1：1：1，尤克里里够了之后导弹和本能保持2：1

红色草，yyds

boss装备 熔岩钻机，最强输出装

附录

A. 绿白输出配装表

focus	red	yellow	bomb	missle	ukulele	instinct
1	0	0	1	0	0	0	0
2	0	0	3	0	1	0	0
3	0	0	5	0	2	0	0
4	0	1	5	0	3	0	0
5	0	3	6	0	4	0	0
6	0	4	7	0	5	0	0
7	0	5	8	0	6	0	0
8	0	6	9	0	7	0	0
9	0	7	10	0	7	0	1
10	0	9	10	0	8	0	1
11	0	9	11	0	9	0	1
12	3	9	6	4	6	0	5
13	3	9	13	0	10	0	2
14	4	9	14	0	11	0	2
15	5	9	14	0	12	0	2
16	6	9	15	0	13	0	2
17	8	9	16	0	13	0	3
18	9	9	17	0	14	0	3
19	10	9	18	0	15	0	3
20	11	9	18	0	16	0	3
21	12	9	19	0	16	0	4
22	14	9	20	0	17	0	4
23	15	9	21	0	18	0	4
24	16	9	22	0	19	0	4
25	14	9	25	0	18	4	1
26	15	9	14	12	11	4	9
27	17	9	27	0	20	4	1
28	18	9	28	0	21	4	1
29	19	9	29	0	21	4	2
30	20	9	29	0	22	4	2
31	21	9	30	0	23	4	2
32	23	9	31	0	24	4	2
33	24	9	32	0	24	4	3
34	25	9	33	0	25	5	3
35	26	9	33	0	26	4	3
36	27	9	34	0	27	5	3
37	29	9	35	0	27	5	4
38	30	9	36	0	28	4	4
39	31	9	37	0	29	4	4
40	32	9	37	0	30	5	4
41	33	9	38	0	30	4	5
42	35	9	39	0	31	4	5
43	36	9	40	0	32	4	5
44	37	9	41	0	33	4	5
45	38	9	41	0	33	4	6
46	39	9	42	0	34	5	6
47	41	9	43	0	35	4	6
48	42	9	44	0	36	4	6
49	43	9	45	0	36	5	7
50	44	9	45	0	37	4	7
51	45	9	47	0	38	4	7
52	47	9	47	0	39	4	7
53	48	9	48	0	39	4	8
54	49	9	49	0	40	5	8
55	50	9	49	0	41	5	8
56	51	9	50	0	42	5	8
57	53	9	51	0	42	5	9
58	54	9	52	0	43	4	9
59	55	9	53	0	44	4	9

B. 绿白黄输出配装表

	focus	red	yellow	bomb	steak	psg	slug	fungus	tough	missle	ukulele	instinct	clover	charged_perforator	molten_perforator	ir_pearl
0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0
1	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0
2	0	0	3	0	0	0	0	0	0	1	0	0	0	0	0	0
3	0	1	3	0	0	0	0	0	0	2	0	1	0	0	1	0
4	0	2	4	0	0	0	0	0	0	3	0	1	0	0	1	0
5	0	3	4	0	0	0	0	0	0	3	0	1	0	0	1	0
6	0	4	5	0	0	0	0	0	0	4	0	1	0	0	1	0
7	0	5	5	0	0	0	0	0	0	2	2	2	0	0	1	0
8	0	6	6	0	0	0	0	0	0	0	4	2	0	0	2	0
9	0	6	6	0	0	0	0	0	0	1	4	2	0	0	2	0
10	0	7	7	0	0	0	0	0	0	1	4	2	0	0	2	0
11	0	8	7	0	0	0	0	0	0	2	5	3	0	0	2	0
12	0	9	8	0	0	0	0	0	0	3	4	3	0	0	3	0
13	0	9	8	0	0	0	0	0	0	3	4	3	0	0	3	0
14	1	9	9	0	0	0	0	0	0	4	5	3	0	0	3	0
15	2	9	9	0	0	0	0	0	0	4	5	4	0	0	3	0
16	3	9	10	0	0	0	0	0	0	5	5	4	0	0	4	0
17	4	9	10	0	0	0	0	0	0	6	5	4	0	0	4	0
18	5	9	11	0	0	0	0	0	0	6	5	4	0	0	4	0
19	6	9	11	0	0	0	0	0	0	7	5	5	0	0	4	0
20	7	9	12	0	0	0	0	0	0	8	4	5	0	0	5	0
21	8	9	12	0	0	0	0	0	0	8	5	5	0	0	5	0
22	9	9	12	0	0	0	0	0	0	9	5	5	0	0	5	0
23	9	9	13	0	0	0	0	0	0	9	5	6	0	0	6	0
24	10	9	14	0	0	0	0	0	0	10	5	6	0	0	6	0
25	11	9	14	0	0	0	0	0	0	11	5	6	0	0	6	0
26	12	9	15	0	0	0	0	0	0	11	5	6	0	0	6	0
27	13	9	15	0	0	0	0	0	0	12	5	7	0	0	6	0
28	14	9	16	0	0	0	0	0	0	13	5	7	0	0	7	0
29	15	9	16	0	0	0	0	0	0	13	5	7	0	0	7	0
30	16	9	17	0	0	0	0	0	0	14	5	7	0	0	7	0
31	17	9	17	0	0	0	0	0	0	14	5	8	0	0	7	0
32	17	9	18	0	0	0	0	0	0	15	5	8	0	0	8	0
33	18	9	18	0	0	0	0	0	0	16	5	8	0	0	8	0
34	20	9	18	0	0	0	0	0	0	16	5	8	0	0	8	0
35	20	9	19	0	0	0	0	0	0	17	5	9	0	0	8	0
36	21	9	20	0	0	0	0	0	0	18	5	9	0	0	9	0
37	22	9	20	0	0	0	0	0	0	18	5	9	0	0	9	0
38	23	9	20	0	0	0	0	0	0	19	5	9	0	0	9	0

Risk of Rain 2 工程师指数流配装

https://heth.ink/Risk-of-Rain-2-ngin/

作者

发布于

2022-03-30

更新于

2022-03-30

Risk of Rain 2 工程师指数流配装

极限DPS

主要机制分析

物品分析

数学模型

极限肉度

机制分析

数学建模

总结

附录

A. 绿白输出配装表

B. 绿白黄输出配装表

作者

发布于

更新于

许可协议

目录

分类

最新文章