Alpha策略中的风险模型——沉默的基石

Alpha策略中的风险模型功能是，预测底层资产预期收益的协方差矩阵，从而在给定预期收益率下最小化组合方差，提升策略夏普比。风险模型的重要程度不亚于收益率模型，但与收益率模型相比，关于搭建风险模型的介绍和讨论却门可罗雀，一方面是由于大多数投资人选择使用商用方案（Barra），另一方面风险模型需要从策略全局考虑问题，不能通过简单的benchmark评估其贡献。本文系统性地介绍了风险模型的定义和实现方案，包括压缩估计、专家因子模型以及数据驱动的统计模型。

协方差估计

最优投资组合

收益率高的投资组合未必好。 现代投资组合理论指出，最优投资组合是在给定组合方差下，能达到最高预期收益率的组合。在只考虑风险资产的情形下，由于每一期投资组合是底层资产的线性组合，所有可行组合的预期收益-方差边界张成双曲线，其上半部分被称为 有效边界(Efficient Frontier) 。所有量化交易策略的研发目标都是接近有效边界，提升与无风险资产组合后的风险收益比。

假设所有风险资产的预期收益\(\mu\)与协方差矩阵\(\Sigma\)已知，权重为\(w\)组合预期收益 \(R_p\) 和方差 \(\sigma^2_p\) 为

$$ R_p = w^T \mu $$

$$ \sigma^2_p = w^T \Sigma w $$

要求解最优权重的目标函数为

$$ \max_w w^T \mu - \frac{\lambda}{2} w^T \Sigma w $$

其中，\(\lambda\)是风险厌恶系数。在无约束条件时，最优权重有解析解

$$ w^* = \frac{1}{\lambda} \Sigma^{-1} \mu $$

综上，最优投资组合权重的求解要求我们对风险资产的预期收益率和协方差矩阵作出估计。对主动管理投资而言，无论是对收益率还是协方差更准确的估计都能最终提升策略夏普比，从而更高效地将投研人员的研究投入转化为超额收益。

困难与挑战

在低信噪比、少样本的金融数据中，协方差预测可谓困难重重。最简单的估计方法是使用历史数据协方差，而首当其冲的是样本量不足。 在正态性和平稳性的假设下，由于估计误差的存在，采用样本协方差矩阵得到的最优投资组合的风险通常会被低估，其模型估计值与真实风险之间的关系满足

$$ \sigma_{\text {true }}=\frac{\sigma_{\text {est }}}{1-(N / T)} $$

当N越来越大时，二者之间的偏差将越来越大。而由于收益率协方差的时变特性，我们注定无法使用非常长周期的历史数据计算样本协方差，在股票Alpha策略中N通常比T高出一个数量级。当股票数量N大于样本观测长度T时，简单协方差矩阵便是一个不满秩的矩阵，因此不能直接对其求逆操作，这使得其在实际应用中大打折扣。

即使有了相对可靠的风险模型用于估计协方差，组合优化中还存在风险模型与收益率模型错位的问题。 由于收益模型和风险模型的错位，它可以被分解成两个部分，其中一个部分是R在由k个风险因子构成的超平面对的投影，另一部分是垂直于该超平面的残差。 这两个部分共同影响了最终的组合优化结果，而垂直于超平面的那部分收益在组合优化中被认为没有任何风险，实则不然，最终使得组合权重低估了这部分风险。 事实上，所有收益预测变量也都附带预期收益率的相关性，俗称“盈亏同源”。因为特质性风险可以被分散投资充分消除， 没有系统性风险的收益率预测变量会导致无风险套利机会的产生， 即便出现这种机会也不会长期稳定存在。

压缩估计

有没有可能通过引入人工先验，从而提高协方差估计的稳定性呢？Ledoit-Wolf（LW）压缩估计是一种用于估计协方差矩阵的方法，特别适用于高维数据和少样本情况。LW压缩估计的主要思想是通过引入一个收缩系数，将样本协方差矩阵与一个特殊的结构化矩阵进行加权平均，从而得到一个更稳定和更可靠的协方差矩阵估计。

具体来说，LW压缩估计的公式如下：

$$ \hat{\Sigma}_{LW} = (1 - \alpha) \cdot S + \alpha F $$

其中，\(\hat{\Sigma}_{LW}\)是LW估计得到的协方差矩阵，\(S\)是样本协方差矩阵，\(\alpha\)是一个收缩系数，\(F\)表示压缩目标。LW估计中的收缩系数 \(\alpha\) 控制着收缩的程度，通常通过经验或交叉验证等方法来确定。当 \(\alpha = 0\) 时，LW估计退化为简单的样本协方差矩阵；当 \(\alpha = 1\) 时，LW估计等于一个特殊的结构化矩阵。压缩矩阵估计的输入非常简单，只需要将个股的历史收益率数据作为输入即可。它不像因子模型的构建一样需要太多的额外信息，其所需信息和模型参数都相对较少

LW 采用 Frobenius 距离定义估计协方差与真实协方差之间的相似度，推导结论是最优压缩系数

$$\alpha^* = \frac{\sum_{i=1}^{N} \sum_{j=1}^{N} \operatorname{Var}\left(s_{i j}\right)-\operatorname{Cov}\left(f_{i j}, s_{i j}\right)}{\sum_{i=1}^{N} \sum_{j=1}^{N} \operatorname{Var}\left(f_{i j}-s_{i j}\right)+\left(\phi_{i j}-\sigma_{i j}\right)^{2}}$$

其中\(E(F_{ij})=\phi_{ij}\)， \(E(S_{ij})=\sigma_{ij}\)

在LW先后发布的三篇论文中，作者分别给出了三种不同的线性压缩目标\(F\)。

1. 等方差模型

$$ F=I *\left(\frac{1}{T} \sum_{i=1}^{N} s_{ii}\right) $$

使用等方差模型相当于人为缩小\(S\)中非对角线元素。

2. 市场指数模型

市场指数模型是采用 CAPM 估计得到的协方差矩阵，最终结果是单因子模型与样本协方差的混合。

$$ F=\sigma_{m}^{2} *\left(\beta \beta^{\prime}\right)+\Delta $$

3. 等相关系数模型

在等相关系数模型中，压缩目标 F 的对角线上的元素与样本协方差对角线上的元素保持一致。而其非对角线上的元素则由相关系数与个股的波动乘积确定。

$$ f_{ii}=s_{ii},f_{ij}=\overline r \sqrt {s_{ii} s_{jj}} $$

其中

$$ \overline{r} = \frac{2}{N(N-1)} \Sigma_{j>i}{\frac{s_{ij}}{\sqrt {s_{ii} s_{jj}}}} $$

专家因子模型

多因子理论创立之初，解释资产价格共同运动便是其主要目的之一。因子模型假设稀疏的因子是导致资产截面收益率差异的内部因素。

$$E(R)=\alpha + \beta \lambda + \epsilon$$

因此只要能准确估计资产在不同因子上的暴露度\(\beta\)和因子协方差关系，就能把原来\(N \times N\) 的矩阵大幅度降维。记

$$ \Beta = [\beta_1 \dots \beta_N ]^T \in \mathbb{R}^{N \times K} $$

为因子暴露，对上式两边取方差

$$ \Sigma = \Beta^T \Sigma_\lambda \Beta + \Delta $$

其中 \(\Sigma_\lambda\) 为因子收益率协方差，\(\Delta\) 为资产特质波动，是一个对角阵。

如果谈论基于多因子的结构化风险模型，Barra模型是绕不过的大山。本节的后半部分介绍以Barra为代表介绍股票因子风险模型。

CNE5模型中包含K个因子，其中一个国家因子，起到截距的作用，P个独热编码的行业因子，以及Q个风格因子。K=1+P+Q。

$$ R = \mathbf{1}\lambda_C + \Beta^I \lambda_I + \Beta^S \lambda_S + \Epsilon $$

Barra多因子模型的一大特点是使用公司特征确定因子暴露的原始值，计算较为简便。如一只股票的过去一年的收益率是20%，那么0.2就是它对动量因子暴露的原始值。接下来需要对原始值进行标准化处理（减去市场组合的因子暴露，再除以标准差），使得市场组合对所有因子暴露为零。

Barra假设个股特质性收益的方差与市值平方根成反比，在每个截面进行截面回归，通过WLS估计求解因子收益率\(\lambda\)。一旦得到因子收益率序列和个股特质性收益率序列，就可以计算个股协方差矩阵。然而，大量实证经验显示，使用历史数据计算难以得到协方差矩阵的准确估计，因此需要通过不同的统计手段对结果进行调整。

作为风险模型，Barra在业界收到广泛认可。作为基于专家因子的风险模型，显著优势在于可解释性较好，其不仅能用于组合优化，还能用于组合收益率、风险的事后解释。

然而，这种结构化风险模型也有天然的缺陷：人力无法确定有多少因子是有影响的，更无法穷尽所有因子，因此最终估计是有偏的。于是人们开始允许残差收益率存在相关性，即 \(\Delta\) 可以不是对角阵，与原假设精确(Exact)因子模型相对，这被称为近似因子模型(Approximate Factor Model)。

统计模型

近年来，基于PCA、自编码器等方法的隐式因子模型日益受到关注。如果说专家因子模型是基于人为假定的稀疏因子分解\(\Sigma\), 而PCA则是直接通过数据驱动的统计手段对\(\Sigma\)进行分解，两者的形式是极其相似的。PCA对历史收益率矩阵的样本协方差 \(\Sigma\) 进行分解:

$$ \Sigma = v^T\lambda v $$

其中 \(v\)是特征向量， \(\lambda\)是特征值。取前k个最大的特征值对应的特征向量作为主成分，那么主成分矩阵 \(v^T \in N \times K\) 就与因子暴露 \(\Beta\) 形式一致。

在估计协方差时，对于因为丢弃特征值而无法解释的那部分方差，PCA假设它们是方差相等的特质波动，直接加到还原协方差的对角线上。PCA方法与上一节的专家因子模型内核完全一致，与压缩估计也有相通之处，因为LW压缩估计等价于先对样本协方差矩阵做特征分解，然后再对由特征值构造的对角阵进行收缩。

而2021年微软提出的Deep Risk Model（DRM）通过设计损失函数，首次将风险因子挖掘规范化为一个监督学习问题，实验也取得不错的效果。

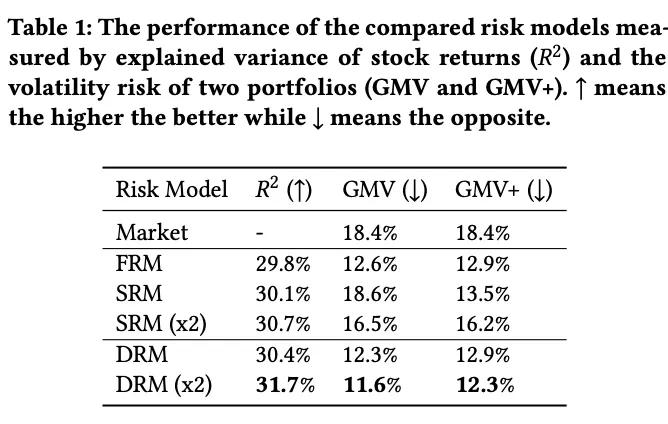
论文设计新的损失函数优化风格因子挖掘的三个目标：

• 解释力 风格因子暴露矩阵是由神经网络习得的 \(R_{\cdot t}=g_\theta(X_{\cdot t})\)，拟合优度\(R^2\)用于描述因子对收益率方差解释度。因此第一项是最大化经验\(R^2\)

$$ R_{\cdot t}^{2}=1-\frac{\left\|\mathrm{y} \cdot t-\mathbf{F}_{\cdot t}\left(\mathbf{F}_{\cdot t}^{\top} \mathbf{F} \cdot t\right)^{-1} \mathbf{F}_{\cdot t}^{\top} \mathbf{y} \cdot t\right\|_{2}^{2}}{\|\mathbf{y} \cdot t\|_{2}^{2}} $$

• 正交性 为了避免挖掘出大量相似度极高的因子，作者通过限制方差膨胀系数(VIF)，使得因子尽量正交。经过推导，作者给出VIF等价形式

$$ \Sigma \text{}{VIF}_i = N \cdot tr((F^TF)^{-1}) $$

• 稳定性 作者定义问题为对未来1～20天解释度的多目标优化，从而使得风格因子有极高的自相关性。

最终模型的优化目标为

$$ \min _{\theta} \frac{1}{T} \sum_{t=1}^{T}\left[\frac{1}{H} \sum_{h=1}^{H} \frac{\left\|\mathbf{y} \cdot, \mathbf{t}+\mathbf{h}-\mathbf{F}_{\cdot t}\left(\mathbf{F}_{\cdot t}^{\top} \mathbf{F}_{\cdot t}\right)^{-1} \mathbf{F}_{\cdot t}^{\top} \mathbf{y} \cdot \mathbf{t}\right\|_{2}^{2}}{\left\|\mathbf{y}_{\cdot, \mathbf{t}+\mathbf{h}}\right\|_{2}^{2}}+\lambda \operatorname{tr}\left(\left(\mathbf{F}_{\cdot t}^{\top} \mathbf{F}_{\cdot t}\right)^{-1}\right)\right] $$

在所有模型中，笔者青睐最后介绍的DRM。首先，其定义简介优雅，输入信息与模型结构都有极高的可拓展性，能够充分利用已知信息，如文本embedding等，而不只是依赖于历史收益率矩阵。其次，DRM模型可以输入alpha预测因子，有助于缓解第一节中提到的错位问题。

参考资料

• 财通证券 “星火”多因子专题报告（八）组合风险控制：协方差矩阵估计方法介绍及比较
• 石川《因子投资》
• Lin, Hengxu, Dong Zhou, Weiqing Liu和Jiang Bian. 2021. 《Deep Risk Model: A Deep Learning Solution for Mining Latent Risk Factors to Improve Covariance Matrix Estimation》. arXiv. http://arxiv.org/abs/2107.05201.