SHAP——理论最优的机器学习解释算法——可能是最简明的解释

SHAP (SHapley Additive exPlanations)基于博弈论，是一种模型无关的机器学习解释方法，既能衡量单次预测结果中的特征贡献，也能聚合局部结果成为对模型的整体解释。SHAP方法在理论上有诸多优异性质，得益于大量工程优化，在实践中也有很强的可操作性，是XAI领域的重要方法。本文主要简介SHAP的基础理论，并给出应用示例。

Shapley值

Shapley值是一个博弈论概念，其提出的初衷是在团队中公平分配利益。设想有p个海盗组成了一个团队，在一次成功的探险后获得了100个金币，怎么公平地分配呢？平均分配显然不合理，而按照能力分配呢——海盗A战力无双就应该多分钱吗，海盗B虽然弱不禁风但是唯一的医生，似乎更加不可或缺？

分配规则还有这样一些限制条件：

• 有效性。每个人贡献分数应该相加等于100，这样才能正好分完100枚金币。
• 对称性。如果有两个人价值一样，那么所得也该一样
• 反事实。如果有个人可有可无，那么他分配的结果是0.
• 可加性。分配100金币的结果，应该等于先分配40，再分配60的结果。

理论证明Shapley值是唯一满足上述条件的解，海盗j的贡献分数是：

$$ \phi_j(val)=\sum_{S\subseteq\{1,\ldots,p\} \backslash \{j\}}\frac{|S|!\left(p-|S|-1\right)!}{p!}\left(val\left(S\cup\{j\}\right)-val(S)\right) $$

踢掉j之后，剩余海盗重组新团队S，可能没有人，也可能是1, 2, 3 … p-1人。val是价值函数，表示不同团队所能取得的收益，并且

$$ val({\{1,\dots, p\}})=100 $$

公式中的归一化系数计算了剔除j后，假定等概率，给定新团队S出现的概率。

$$ \frac{|S|!\left(p-|S|-1\right)!}{p!} $$

而 \(val\left(S\cup{j}\right)-val(S)\) 计算j加入新团队后，能多获取多少金币，即增量贡献。

SHAP定义

我们考虑一个线性模型 \(\hat{f}(x)=\beta_0+\beta_{1}x_{1}+\ldots+\beta_{p}x_{p}\) ，特征 \(x_j\) 对输出结果的影响，显然是只和它对应的系数有关的 \(\beta_i x_j\)，相应的，特征 \(x_j\)的增量贡献是

$$ \phi_j(\hat{f})=\beta_{j}x_j-\beta_{j}E(X_{j}) $$

总的要分配的价值是

$$ \begin{aligned} \sum_{j=1}^{p}\phi_j(\hat{f})=&\sum_{j=1}^p(\beta_{j}x_j-E(\beta_{j}X_{j}))\\=& (\beta_0+\sum_{j=1}^p\beta_{j}x_j)-(\beta_0+\sum_{j=1}^{p}E(\beta_{j}X_{j}))\\=& \hat{f}(x)-E(\hat{f}(X)) \end{aligned} $$

由于我们在其他非线性模型（比如集成模型）中没有类似的权重，因此我们需要一个不同的解决方案。第一节中我们了解了如何用Shapley值计算一次联盟博弈过程，如果把一次机器学习模型预测过程也看做上述探险，那么就是SHAP的解法。把每个特征视作团队成员，这是符合直觉的，核心是定义价值函数val。在SHAP算法中，定义了

$$ val_{x}(S)=\int\hat{f}(x_{1},\ldots,x_{p})d\mathbb{P}_{x\notin{}S}-E_X(\hat{f}(X)) $$

模型输出值可以视作特征贡献的线性叠加，shap解释满足可加性和有效性。

$$ \hat{f}(x)=\phi_0+\sum_{j=1}^M\phi_jx_j'=E_X(\hat{f}(X))+\sum_{j=1}^M\phi_j $$

然而现实中要解释的特征贡献往往是交互影响的，精确shap值计算复杂度极高以至于无法实现，因此原文还总结和创新了数种模型无关、模型相关的近似算法。

应用与可视化

shap是SHAP算法的开源实现，提供了简洁的api和精美的可视化。

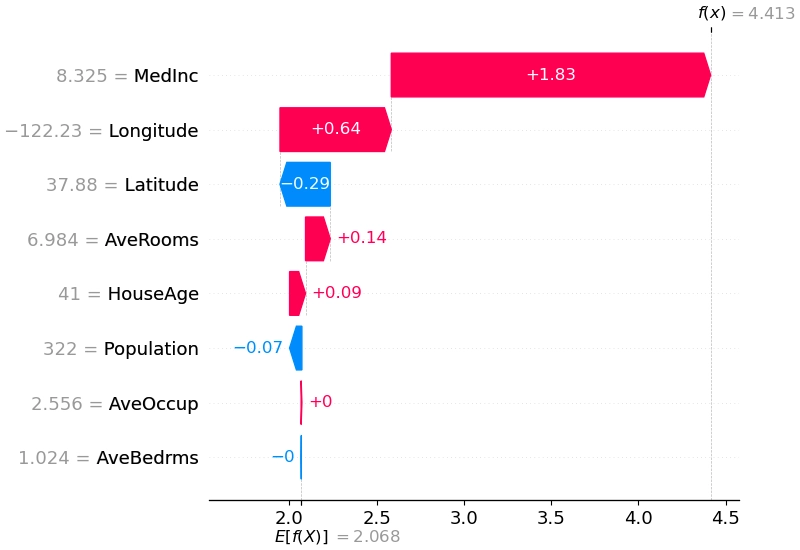
首先是单次预测的解释，由于满足有效性和可加性，可以画出瀑布图展示不同特征的精确贡献

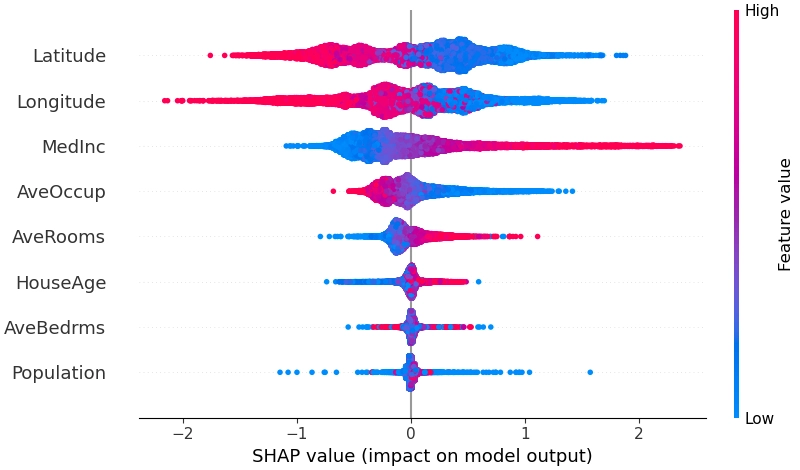
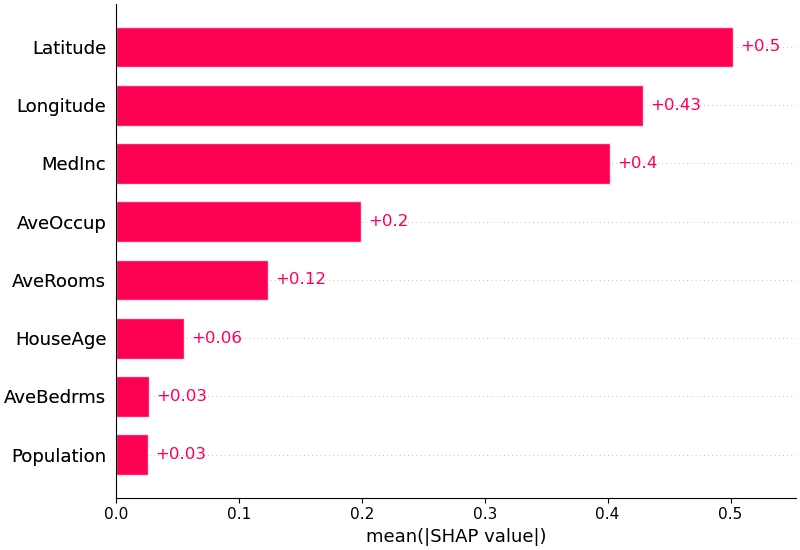
统计shap值整体分布，可以得到关于模型的整体解释

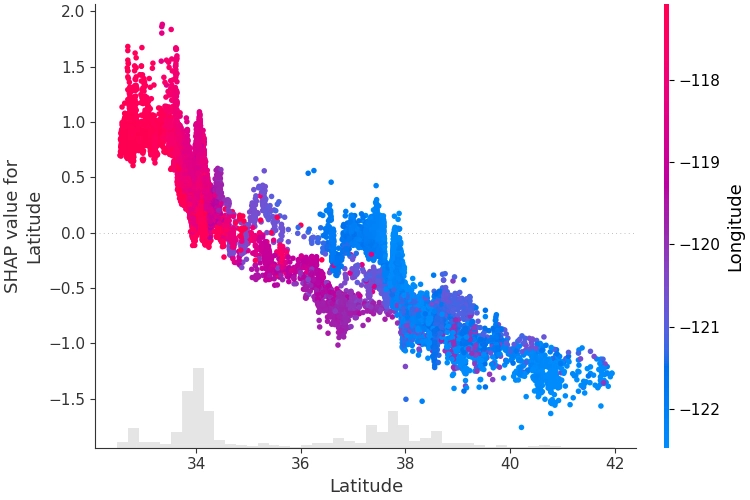
还能够观察不同特征间的交互作用

参考资料

• Lundberg, S.M., Lee, S.-I.: A Unified Approach to Interpreting Model Predictions. In: Advances in Neural Information Processing Systems. Curran Associates, Inc. (2017).
• interpretable-ml-book SHAP (SHapley Additive exPlanations) https://christophm.github.io/interpretable-ml-book/shap.html