k均值聚类：收敛性证明与两种变体

本文首先证明了k-means算法的收敛性，与网上已有资料相比较为简洁明了。后半部分讨论了k-means结合GMM与RPCL算法思想后产生的两种变体。本文不适合初步了解k-means算法阅读。

算法收敛性证明

损失函数

$$ J=\sum_{i=1}^k\sum_{x\in{C_i}}||x-\mu_i||_2^2 $$

k-means算法伪代码[1]如下

要证明k-means算法收敛，充分条件是损失函数单调且有界

单调性

算法分为两步，第一步就近分配x的簇，第二步重新计算均值向量。
首先考虑第一步
如果\(x_i\)簇不变，显然损失函数不增。
如果\(x_i\)簇改变，不失一般性，考虑

$$ J'=J-||x_i-\mu_k||_2^2+||x_i-\mu_{k'}||_2^2 $$

因为

$$ ||x_i-\mu_k||_2 \geq ||x_i-\mu_{k'}||_2 $$

所以损失函数不增。

接着考虑第二步
不失一般性，考虑一个簇的损失函数

$$ J_i=\sum_{x\in{C_i}}||x-\mu_i||_2^2 $$

令

$$ \frac{\partial J_i}{\partial \mu_i}=0 $$

计算得此时

$$ \mu_i= \frac{1}{|C_i|}\sum_{x\in{C_i}}x=\mu'_i $$

更新后的均值向量位于函数最小值点，因此算法中更新这一步不会导致损失函数增加

综上所述，k-means算法中损失函数单调递减。

有界

显然有界。

综上，k-means算法收敛性证明完毕。

k-means vs. GMM

与k-means用原型向量来刻画聚类结构不同，高斯混合聚类采用概率模型来表达聚类原型[1]：

$$ p_{\theta^{t}}(C_k|x_i) = \frac{p_{\theta^{t}}(C_k)p_{\theta^{t}}(x_i|C_k)}{\sum_j p_{\theta^{t}}(C_j)p_{\theta^{t}}(x_i|C_j)} $$

从这个角度来看，k-means也假定了一种概率分布[2]：

$$ p(C_j|x_i) = 1 \quad \mathrm{if} \quad \lVert x_i - \mu_j \rVert^2_2 = \min_k \lVert x_i - \mu_k \rVert^2_2 \\p(C_j|x_i) = 0 \quad \mathrm{otherwise} $$

通过修改这种概率分布，可以设计出一种介于k-means与GMM之间的算法，例如softmax：

$$ p(C_j|x_i) = \frac{\exp(- \alpha\lVert x_i - \mu_j \rVert^2_2)}{\sum_k \exp(- \alpha\lVert x_i - \mu_k \rVert^2_2)} $$

新的损失函数

$$ J = \sum_i \sum_j p(C_j|x_i) \lVert x_i - \mu_j \rVert^2 $$

计算偏导

$$ \frac{\partial{J}}{\partial{\mu_j}} = -2 \sum_i p(C_j|x_i) (x_i - \mu_j) $$

令偏导为零,得到更新均值向量的公式

$$ \mu_j = \frac{\sum_i p(C_j|x_i) x_i}{\sum_i p(C_j|x_i) } $$

对于原来[1]的k-means伪代码，只要把第5、6行的距离改为后验概率，把第10行换成计算上述公式即可。

优点
1.降低对异常值敏感度
2.是k-means算法的推广形式
3.实现仍然比较简单

缺点
1.需要调整更多的超参数（α）
2.对初始值敏感

k-means vs. RPCL

k-means中可以引入竞争学习的思想，自动学习聚类簇数。
定义

$$ vector_i=\frac{1}{|C_i|}\sum_{x\in{C_i}}x-\mu_i $$

结合RPCL的思想，修改更新均值向量的规则:

$$ \mu'_i=\mu_i+learnrate \cdot vector_i\\ \mu'_k=\mu_k-learnrate \cdot penalty \cdot vector_i$$

其中

$$ ||\mu_i-\mu_k||^2=min_{j \ne i}||\mu_i-\mu_j||^2\\ learnrate=const.,penalty=const. $$

如果没有x的簇被改变则算法自动终止，与原来的k-means算法一致。仅修改原来的第二步，最相近的均值向量会自动分离，实现自动确定分类簇数的效果。

def k_means_with_RPCL(dataSet, k, dist_func=distEclud, 
                        createCent=randCent, lr=1, penalty=0.5):
    m = shape(dataSet)[0]
    dist_to_mu = mat(zeros((m,2)))
    centroids = createCent(dataSet, k)
    # 用来判断聚类是否已经收敛,false为收敛
    clusterChanged = True   
    while clusterChanged:
        clusterChanged = False
        # 把每一个数据点划分到离它最近的中心点
        for i in range(m):  
            minDist = inf  # 最小
            minIndex = -1
            for j in range(k):
                # 算第i个数据点到第k个聚类中心的距离
                distJI = dist_func(centroids[j, :], dataSet[i, :])  
                if distJI < minDist:
                    minDist = distJI
                    # 如果第i个数据点到第j个中心点更近，则将i归属为j
                    minIndex = j 
            if dist_to_mu[i, 0] != minIndex : clusterChanged = True
            # 并将第i个数据点的分配情况存入字典
            dist_to_mu[i, :] = minIndex, minDist**2  

        for cent in range(k):   # 重新计算中心点
            secDist = inf  # 第二小
            secIndex = -1
            for i in range(k):
                if i != cent:
                    dist = dist_func(centroids[cent, :], centroids[i, :])
                    if dist < secDist:
                        secDist = dist
                        secIndex = i


            ptsInClust = dataSet[nonzero(dist_to_mu[:, 0] == cent)[0]]
            
            vector=(mean(ptsInClust, axis=0) - centroids[cent, :])
            centroids[cent, :] = centroids[cent, :] + lr * vector
            centroids[secIndex, :] = centroids[secIndex, :] - lr * penalty * vector

聚类结果
设置k=5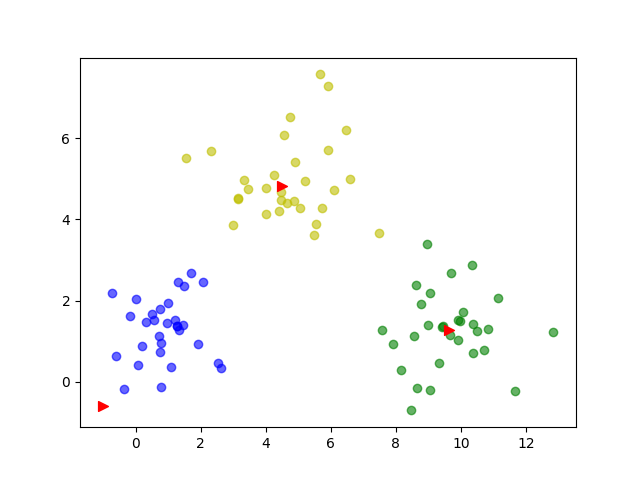

设置k=6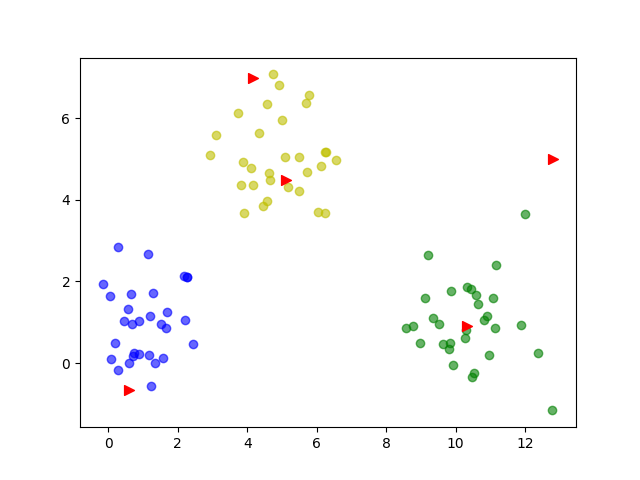

达到了预期效果

参考资料
[1.]周志华. 机器学习[J]. 2016
[2.]EM 算法与 K-means 和 GMM 聚类 https://sighsmile.github.io/2019-11-22-EM-KMeans-GMM/